练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】已知点A（0，－2），椭圆E： （a>b>0）的离心率为，F是椭圆E的右焦点，直线AF的斜率为，O为坐标原点．

    （1）求E的方程；

    （2）设过点A的动直线l与E相交于P，Q两点，当△OPQ的面积最大时，求l的方程．

    【答案】（1）（2）或

    【解析】

    试题分析：（Ⅰ）通过离心率得到a、c关系，通过A求出a，即可求E的方程；（Ⅱ）设直线l：y=kx-2，设P，Q将y=kx-2代入，利用△＞0，求出k的范围，利用弦长公式求出|PQ|，然后求出△OPQ的面积表达式，利用换元法以及基本不等式求出最值，然后求解直线方程

    试题解析：（1）设，由条件知，又，所以

    所以E的方程为

    （2）当轴时不合题意，故可设

    将代入得

    当即时

    从而

    又点O到直线的距离为

    所以的面积为，设，则

    ，当且仅当时即时等号成立，满足，所以当面积最大值

    直线方程为或

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】已知由方程kx2－8x＋16＝0的根组成的集合A只有一个元素，试求实数k的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某中学调查了某班全部45名同学参加书法社团和演讲社团的情况，数据如下表：（单位：人）

    参加书法社团

    未参加书法社团

    参加演讲社团

    8

    5

    未参加演讲社团

    2

    30

    （I）从该班随机选1名同学，求该同学至少参加上述一个社团的概率；

    （II） 在既参加书法社团又参加演讲社团的8名同学中，有5名男同学，3名女同学，现从这5名男同学和3名女同学中各随机选1人，求被选中且未被选中的概率。

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】甲、乙两人同时报考某一所大学，甲被录取的概率为0.6，乙被录取的概率为0.7，两人是否被录取互不影响，则其中至少有一人被录取的概率为( )

    A. 0.12 B. 0.42 C. 0.46 D. 0.88

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】840和1 764的最大公约数是_____.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，直三棱柱ABC－A1B1C1中，D、E分别是AB、BB1的中点．

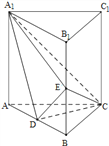
    （Ⅰ）证明：BC1∥平面A1CD；

    （Ⅱ）AA1＝AC＝CB＝2，AB＝，求三棱锥C﹣A1DE的体积．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】“三角形的外角至少有两个钝角”的否定是__________.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】“p或q”为真命题是“p且q”为真命题的________条件.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】设函数,其中为实数.

    （1）若在上是单调减函数, 且在上有最小值, 求的取值范围；

    （2）若在上是单调增函数, 试求的零点个数, 并证明你的结论.

    查看答案和解析>>

    同步练习册答案