
 ,则m-n= .
,则m-n= .
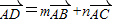 ,求出m和n的值,即可求得m-n的值.
,求出m和n的值,即可求得m-n的值.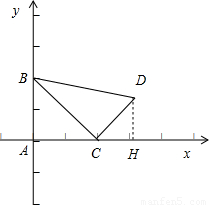 解:由题意可得BC=
解:由题意可得BC=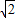 AB=2
AB=2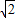 ,CD=BC•tan∠CBD=2
,CD=BC•tan∠CBD=2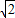 tan30°=
tan30°=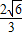 ,
,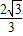 ,DH=CDsin(180°-135°)=
,DH=CDsin(180°-135°)=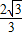 .
.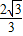 ,
,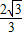 ),再由题意可得B(0,2),C(2,0).
),再由题意可得B(0,2),C(2,0).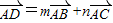 ,
,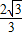 ,
,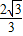 )=m(0,2)+n(2,0)=(2n,2m),
)=m(0,2)+n(2,0)=(2n,2m),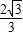 =2n,
=2n,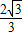 =2m,∴m=
=2m,∴m=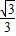 ,n=1+
,n=1+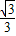 ,∴m-n=-1,
,∴m-n=-1,

科目:高中数学 来源: 题型:
 (考生注意:请在下列三题中任选一题作答,如果多做,则按所做的第一题评分)
(考生注意:请在下列三题中任选一题作答,如果多做,则按所做的第一题评分)| BD |
| DA |
|
查看答案和解析>>
科目:高中数学 来源: 题型:
 (A)(不等式选做题)不等式|x+1|-|x-2|>2的解集为
(A)(不等式选做题)不等式|x+1|-|x-2|>2的解集为| 3 |
| 2 |
| 3 |
| 2 |
| 18 |
| 5 |
| 18 |
| 5 |
|
查看答案和解析>>
科目:高中数学 来源: 题型:
 (A)(几何证明选讲选做题)如图,已知Rt△ABC的两条直角边AC,BC的长分别为3cm,4cm,以AC为直径作圆与斜边AB交于点D,则BD的长为=
(A)(几何证明选讲选做题)如图,已知Rt△ABC的两条直角边AC,BC的长分别为3cm,4cm,以AC为直径作圆与斜边AB交于点D,则BD的长为=| 16 |
| 5 |
| 16 |
| 5 |
|
| π |
| 3 |
| 3 |
| 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:
 (2013•汕头二模)如图,已知Rt△ABC的两条直角边AC,BC的长分别为3cm,4cm,以AC边为直径与AB交于点D,则三角形ACD的面积为
(2013•汕头二模)如图,已知Rt△ABC的两条直角边AC,BC的长分别为3cm,4cm,以AC边为直径与AB交于点D,则三角形ACD的面积为| 54 |
| 25 |
| 54 |
| 25 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com