
【题目】已知椭圆![]() :
:![]() 的左、右焦点与其短轴的一个端点是等边三角形的三个顶点,点
的左、右焦点与其短轴的一个端点是等边三角形的三个顶点,点![]() 在椭圆上,直线
在椭圆上,直线![]() 与椭圆交于
与椭圆交于![]() ,
,![]() 两点,与
两点,与![]() 轴,
轴,![]() 轴分别交于点
轴分别交于点![]() ,
,![]() ,且
,且![]() ,点
,点![]() 是点
是点![]() 关于
关于![]() 轴的对称点,
轴的对称点,![]() 的延长线交椭圆于点
的延长线交椭圆于点![]() ,过点
,过点![]() ,
,![]() 分别作
分别作![]() 轴的垂线,垂足分别为
轴的垂线,垂足分别为![]() ,
,![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)是否存在直线![]() ,使得点
,使得点![]() 平分线段
平分线段![]() ?若存在,求出直线
?若存在,求出直线![]() 的方程,若不存在请说明理由.
的方程,若不存在请说明理由.
【答案】(1)![]() ;(2)答案见解析.
;(2)答案见解析.
【解析】试题分析: (1)由正三角形的高与边长的关系可求出![]() ,再由点
,再由点![]() 在椭圆上,可求出
在椭圆上,可求出![]() 的值,从而求出椭圆方程; (2)假设存在,由直线方程可求出
的值,从而求出椭圆方程; (2)假设存在,由直线方程可求出![]() 点的坐标,由已知条件可求出
点的坐标,由已知条件可求出![]() 点的坐标,设
点的坐标,设![]() 联立直线与椭圆的方程,消去
联立直线与椭圆的方程,消去![]() ,得到关于
,得到关于![]() 的一元二次方程,由韦达定理可求出
的一元二次方程,由韦达定理可求出![]() 的表达式以及直线
的表达式以及直线![]() 的斜率,联立直线
的斜率,联立直线![]() 与椭圆方程,可求出
与椭圆方程,可求出![]() 的表达式,进而求出
的表达式,进而求出![]() 的表达式, 由
的表达式, 由![]() 平分线段
平分线段![]() ,求出
,求出![]() 的值,得出直线方程.
的值,得出直线方程.
试题解析:(1)由题意知![]() ,即
,即![]() ,
,![]() ,即
,即![]() ,
,
∵![]() 在椭圆上,∴
在椭圆上,∴![]() ,
,
![]()
所以椭圆![]() 方程为
方程为![]() .
.
(2)存在
设![]() ,∵
,∵![]()
∴![]() ,
,![]()
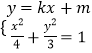 ∴
∴![]() ①
①
∴![]() ,
,![]()
![]()
联立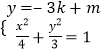 ∴
∴![]() ②
②
∴![]()
∴![]()
∴![]()
若![]() 平分线段
平分线段![]() ,则
,则![]()
即![]() ,
,![]() , ∴
, ∴![]()
∵![]() 把①,②代入,得
把①,②代入,得![]()
所以直线![]() 的方程为
的方程为![]() 或
或![]()
点睛:本题主要考查了椭圆的方程以及直线与椭圆的位置关系,属于中档题.第一问求椭圆方程很容易,大部分学生能做对; 在第二问中,假设存在, 当点![]() 平分线段
平分线段![]() ,
,![]() 点为
点为![]() 的中点,利用中点坐标公式,求出
的中点,利用中点坐标公式,求出![]() 的值,得出直线方程.注意本题涉及的点线位置关系比较复杂,容易弄错.
的值,得出直线方程.注意本题涉及的点线位置关系比较复杂,容易弄错.


科目:高中数学 来源: 题型:
【题目】宁德市某汽车销售中心为了了解市民购买中档轿车的意向,在市内随机抽取了100名市民为样本进行调查,他们月收入(单位:千元)的频数分布及有意向购买中档轿车人数如下表:
月收入 | [3,4) | [4,5) | [5,6) | [6,7) | [7,8) | [8,9) |
频数 | 6 | 24 | 30 | 20 | 15 | 5 |
有意向购买中档轿车人数 | 2 | 12 | 26 | 11 | 7 | 2 |
将月收入不低于6千元的人群称为“中等收入族”,月收入低于6千元的人群称为“非中等收入族”.
(Ⅰ)在样本中从月收入在[3,4)的市民中随机抽取3名,求至少有1名市民“有意向购买中档轿车”的概率.
(Ⅱ)根据已知条件完善下面的2×2列联表,并判断有多大的把握认为有意向购买中档轿车与收入高低有关?
非中等收入族 | 中等收入族 | 总计 | |||||
有意向购买中档轿车人数 | 40 | ||||||
无意向购买中档轿车人数 | 20 | ||||||
总计 | 100 | ||||||
| 0.10 | 0.05 | 0.010 | 0.005 | |||
| 2.706 | 3.841 | 6.635 | 7.879 | |||
附:
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知在图1所示的梯形![]() 中,
中,![]() ,
,![]() 于点
于点![]() ,且
,且![]() .将梯形
.将梯形![]() 沿
沿![]() 对折,使平面
对折,使平面![]() 平面
平面![]() ,如图2所示,连接
,如图2所示,连接![]() ,取
,取![]() 的中点
的中点![]() .
.

(1)求证:平面![]() 平面
平面![]() ;
;
(2)在线段![]() 上是否存在点
上是否存在点![]() ,使得直线
,使得直线![]() 平面
平面![]() ?若存在,试确定点
?若存在,试确定点![]() 的位置,并给予证明;若不存在,请说明理由;
的位置,并给予证明;若不存在,请说明理由;
(3)设![]() ,求三棱锥
,求三棱锥![]() 的体积.
的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某儿童乐园在“六一”儿童节推出了一项趣味活动.参加活动的儿童需转动如图所示的转盘两次,每次转动后,待转盘停止转动时,记录指针所指区域中的数.设两次记录的数分别为x,y.奖励规则如下:
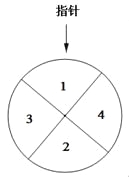
①若![]() ,则奖励玩具一个;
,则奖励玩具一个;
②若![]() ,则奖励水杯一个;
,则奖励水杯一个;
③其余情况奖励饮料一瓶.
假设转盘质地均匀,四个区域划分均匀.小亮准备参加此项活动.
(Ⅰ)求小亮获得玩具的概率;
(Ⅱ)请比较小亮获得水杯与获得饮料的概率的大小,并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】“杨辉三角”又称“贾宪三角”,是因为贾宪约在公元1050年首先使用“贾宪三角”进行高次开方运算,而杨辉在公元1261年所著的《详解九章算法》一书中,记录了贾宪三角形数表,并称之为“开方作法本源”图.下列数表的构造思路就源于“杨辉三角”.该表由若干行数字组成,从第二行起,每一行中的数字均等于其“肩上”两数之和,表中最后一行仅有一个数,则这个数是 ( )
2017 2016 2015 2014……6 5 4 3 2 1
4033 4031 4029…………11 9 7 5 3
8064 8060………………20 16 12 8
16124……………………36 28 20
………………………
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】【2018湖南(长郡中学、株洲市第二中学)、江西(九江一中)等十四校高三第一次联考】已知函数![]() (其中
(其中![]() 且
且![]() 为常数,
为常数, ![]() 为自然对数的底数,
为自然对数的底数, ![]() ).
).
(Ⅰ)若函数![]() 的极值点只有一个,求实数
的极值点只有一个,求实数![]() 的取值范围;
的取值范围;
(Ⅱ)当![]() 时,若
时,若![]() (其中
(其中![]() )恒成立,求
)恒成立,求![]() 的最小值
的最小值![]() 的最大值.
的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com