练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】如图，点E为正方形ABCD边CD上异于点C，D的动点，将△ADE沿AE翻折成△SAE，使得平面SAE⊥平面ABCE，则下列三个说法中正确的个数是（ ）

    ①存在点E使得直线SA⊥平面SBC

    ②平面SBC内存在直线与SA平行

    ③平面ABCE内存在直线与平面SAE平行

    A．0 B．1 C．2 D．3

    【答案】B

    【解析】

    试题分析：对于命题①，若直线SA⊥平面SBC，则直线SA与平面SBC均垂直，则SA⊥BC，又由AD∥BC，则SA⊥AD，这与为锐角矛盾，所以命题①不正确；对于命题②，因为平面直线，故平面内的直线与相交或异面，所以命题②不正确；对于命题③，取的中点，则CF∥AE，由线面平行的判定定理可得CF∥平面SAE，所以命题③正确，故应选.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】已知函数.

    （Ⅰ）讨论的单调性；

    （Ⅱ）当时，设，若存在，，使，求实数的取值范围.（为自然对数的底数，）

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，三棱锥A－BCD中，AB⊥平面BCD，CD⊥BD .

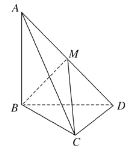
    （1）求证：CD⊥平面ABD；

    （2）若AB＝BD＝CD＝1，M为AD中点，求三棱锥A－MBC的体积．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】从某小区随机抽取40个家庭，收集了这40个家庭去年的月均用水量（单位：吨）的数据，整理得到频数分布表和频率分布直方图.

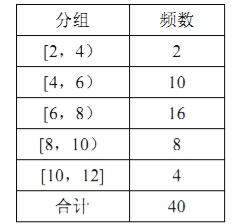
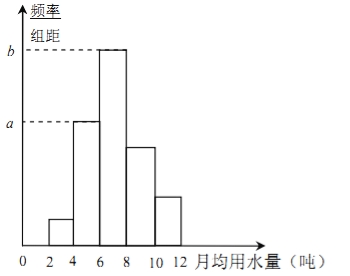
    （1）求频率分布直方图中的值；

    （2）从该小区随机选取一个家庭，试估计这个家庭去年的月均用水量不低于6吨的概率；

    （3）在这40个家庭中，用分层抽样的方法从月均用水量不低于6吨的家庭里抽取一个容量为7的样本，将该样本看成一个总体，从中任意选取2个家庭，求其中恰有一个家庭的月均用水量不低于8吨的概率.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】心理学家发现，学生的接受能力依赖于老师引入概念和描述问题所用的时间，上课开始时，学生的兴趣激增，中间有一段不太长的时间，学生的兴趣保持较理想的状态，随后学生的注意力开始分散，并趋于稳定．分析结果和实验表明，设提出和讲述概念的时间为（单位：分），学生的接受能力为 （值越大，表示接受能力越强），

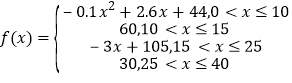
    （1）开讲后多少分钟，学生的接受能力最强？能维持多少时间？

    （2）试比较开讲后5分钟、20分钟、35分钟，学生的接受能力的大小；（3）若一个数学难题，需要56的接受能力以及12分钟时间，老师能否及时在学生一直达到所需接受能力的状态下讲述完这个难题？

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，在三棱锥中，，.

    （Ⅰ）求证： （Ⅱ）求二面角的大小.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】为了对某课题进行研究，用分层抽样方法从三所高校的相关人员中，抽取若干人组成研究小组，有关数据见下表（单位：人）

    高校

    相关人数

    抽取人数

    A

    18


    B

    36

    2

    C

    54


    （Ⅰ）求，；

    （Ⅱ）若从高校抽取的人中选2人作专题发言，求这二人都来自高校的概率.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某城市100户居民的月平均用电量（单位：度），以，，，，，，分组的频率分布直方图如图：

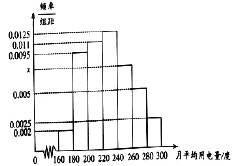
    （Ⅰ）求直方图中的值；

    （Ⅱ）求月平均用电量的众数和中位数；

    （Ⅲ）在月平均用电量为，，，的四组用户中，用分层抽样的方法抽取11户居民，则月平均用电量在的用户中应抽取多少户？

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知f（x）＝－3x2＋a（6－a）x＋6.

    （1）解关于a的不等式f（1）>0；

    （2）若不等式f（x）>b的解集为（－1,3），求实数a，b的值．

    查看答案和解析>>

    同步练习册答案