
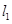 过点
过点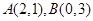 ,直线
,直线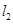 的斜率为
的斜率为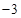 且过点
且过点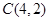 .
.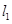 、
、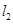 的交点
的交点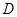 的坐标;
的坐标;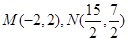 ,若直线
,若直线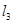 过点
过点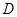 且与线段
且与线段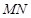 相交,求直线
相交,求直线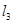 的斜率
的斜率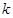 的取值范围.
的取值范围.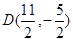 ;(2)
;(2)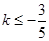 或
或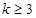 .
.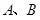 两点的坐标求出斜率
两点的坐标求出斜率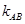 ,然后由直线的点斜式写出直线
,然后由直线的点斜式写出直线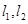 的方程,最后联立方程求解即可得到交点
的方程,最后联立方程求解即可得到交点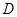 的坐标;(2)法一:先由点斜式写出直线
的坐标;(2)法一:先由点斜式写出直线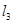 的方程
的方程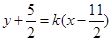 ,由
,由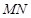 两点的坐标写出线段
两点的坐标写出线段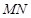 的方程
的方程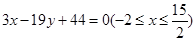 ,联立这两个方程,求出交点的横坐标
,联立这两个方程,求出交点的横坐标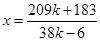 ,然后求解不等式
,然后求解不等式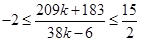 即可得到
即可得到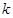 的取值范围;法二:采用数形结合,先分别求出边界直线
的取值范围;法二:采用数形结合,先分别求出边界直线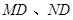 的斜率,由图分析就可得到
的斜率,由图分析就可得到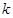 的取值范围.
的取值范围.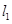 过点
过点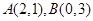
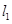 的方程为
的方程为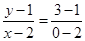 ,即
,即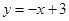 2分
2分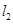 的斜率为
的斜率为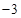 且过点
且过点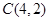
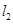 的方程为
的方程为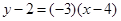 ,即
,即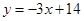 4分
4分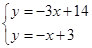 ,解得
,解得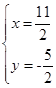 即
即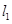 、
、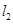 的交点
的交点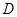 坐标为
坐标为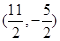 6分
6分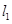 的方程的方程时还可以利用点斜式方程或一般式方程形式求解
的方程的方程时还可以利用点斜式方程或一般式方程形式求解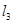 的方程为
的方程为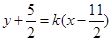 7分
7分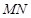 的方程为
的方程为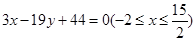 8分
8分 且与线段
且与线段 相交
相交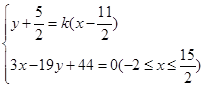
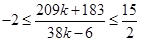 10分
10分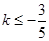 或
或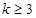
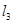 的斜率
的斜率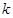 的取值范围为
的取值范围为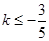 或
或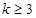 12分
12分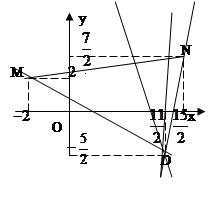
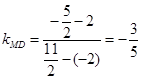 8分
8分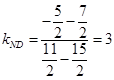 9分
9分 的斜率
的斜率 的取值范围为
的取值范围为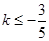 或
或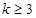 12分.
12分.

 名校课堂系列答案
名校课堂系列答案湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com