
【题目】已知在极坐标系中曲线C的极坐标方程为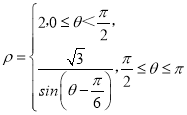 .
.
(1)求曲线C与极轴所在直线围成图形的面积;
(2)设曲线C与曲线ρsinθ=1交于A,B,求|AB|.
【答案】(1)![]() ;(2)2
;(2)2![]() .
.
【解析】
(1)直接利用转换关系,将曲线C的极坐标方程转化为直角坐标方程,得到曲线C与极轴所在直线围成的图形是一个半径为2的![]() 圆周及一个两直角边分别为2与2
圆周及一个两直角边分别为2与2![]() 的直角三角形,即可求得面积.
的直角三角形,即可求得面积.
(2)联立方程组,分别求出A和B的坐标,再利用两点间的距离公式求出结果.
(1)因为曲线C的极坐标方程为 ,
,
所以当![]() 时,
时,![]() ,
,
当![]() 时,x
时,x![]() ,
,
所以曲线C与极轴所在直线围成的图形是一个半径为2的![]() 圆周及一个两直角边分别为2与2
圆周及一个两直角边分别为2与2![]() 的直角三角形,
的直角三角形,
如图所示:

所以![]() .
.
(2)因为曲线C与曲线ρsinθ=1交于A,B,
由![]() ,得A(2,
,得A(2,![]() ),转换为直角坐标为A(
),转换为直角坐标为A(![]() ).
).
极坐标方程ρsinθ=1转换为直角坐标方程为y=1,
极坐标方程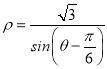 转换为直角坐标方程为x
转换为直角坐标方程为x![]() ,
,
所以B(![]() ),
),
所以|AB|=![]() .
.


科目:高中数学 来源: 题型:
【题目】如图,四边形ABCD是直角梯形,AB=2CD=2PD=2,PC![]() ,且有PD⊥AD,AD⊥CD,AB∥CD.
,且有PD⊥AD,AD⊥CD,AB∥CD.

(1)证明:PD⊥平面ABCD;
(2)若四棱锥P﹣ABCD的体积为![]() ,求四棱锥P﹣ABCD的表面积.
,求四棱锥P﹣ABCD的表面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
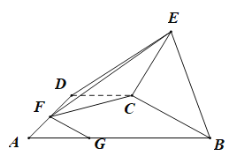
【题目】如图,在直角梯形![]() 中,
中,![]() ,
,![]() ,平面
,平面![]() 平面
平面![]() ,
,![]() ,
,![]() ,
,![]() 分别在线段
分别在线段![]() 和
和![]() 上,且
上,且![]() ,
,![]() 是等腰直角三角形.
是等腰直角三角形.
(1)若![]() ,求证:
,求证:![]() 平面
平面![]() .
.
(2)![]() ,是否存在
,是否存在![]() ,使得
,使得![]() 与平面
与平面![]() 所成的角的正弦值为
所成的角的正弦值为![]() ?若存在,求出
?若存在,求出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在全面建成小康社会的决胜阶段,让贫困地区同全国人民共同进入全面小康社会是我们党的庄严承诺.在“脱真贫、真脱贫”的过程中,精准扶贫助推社会公平显得尤其重要.若某农村地区有200户贫困户,经过一年扶贫后,对该地区的“精准扶贫”的成效检查验收.从这200户贫困户中随机抽出50户,对各户的人均年收入(单位:千元)进行调查得到如下频数表:
人均年收入 |
|
|
|
|
|
|
频数 | 2 | 3 | 10 | 20 | 10 | 5 |
若人均年收入在4000元以下的判定为贫困户,人均年收入在4000元~8000元的判定为脱贫户,人均年收入达到8000元的判定为小康户.
(1)用样本估计总体,估计该地区还有多少户没有脱贫;
(2)为了了解未脱贫的原因,从抽取的50户中用分层抽样的方法抽10户进行调研.
①贫困户、脱贫户、小康户分别抽到的人数是多少?
②从被抽到的脱贫户和小康户中各选1人做经验介绍,求小康户中人均年收入最高的一户被选到的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直三棱柱ABC﹣A1B1C1中,平面ABC是下底面.M是BB1上的点,AB=3,BC=4,AC=5,CC1=7,过三点A、M、C1作截面,当截面周长最小时,截面将三棱柱分成的上、下两部分的体积比为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下图是2020年2月15日至3月2日武汉市新增新冠肺炎确诊病例的折线统计图.则下列说法不正确的是( )

A.2020年2月19日武汉市新增新冠肺炎确诊病例大幅下降至三位数
B.武汉市在新冠肺炎疫情防控中取得了阶段性的成果,但防控要求不能降低
C.2020年2月19日至3月2日武汉市新增新冠肺炎确诊病例低于400人的有8天
D.2020年2月15日到3月2日武汉市新增新冠肺炎确诊病例最多的一天比最少的一天多1549人
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】据相关数据统计,2019年底全国已开通![]() 基站13万个,部分省市的政府工作报告将“推进
基站13万个,部分省市的政府工作报告将“推进![]() 通信网络建设”列入2020年的重点工作,今年一月份全国共建基站3万个.
通信网络建设”列入2020年的重点工作,今年一月份全国共建基站3万个.
(1)如果从2月份起,以后的每个月比上一个月多建设2000个,那么,今年底全国共有基站多少万个.(精确到0.1万个)
(2)如果计划今年新建基站60万个,到2022年底全国至少需要800万个,并且,今后新建的数量每年比上一年以等比递增,问2021年和2022年至少各建多少万个オ能完成计划?(精确到1万个)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了增强学生的环境意识,某中学随机抽取了50名学生举行了一次环保知识竞赛,本次竞赛的成绩(得分均为整数,满分100分)整理,制成下表:
成绩 |
|
|
|
|
|
|
频数 | 2 | 3 | 14 | 15 | 14 | 4 |
(1)作出被抽查学生成绩的频率分布直方图;
(2)若从成绩在![]() 中选一名学生,从成绩在
中选一名学生,从成绩在![]() 中选出2名学生,共3名学生召开座谈会,求
中选出2名学生,共3名学生召开座谈会,求![]() 组中学生
组中学生![]() 和
和![]() 组中学生
组中学生![]() 同时被选中的概率?
同时被选中的概率?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com