
【题目】某教育培训中心共有25名教师,他们全部在校外住宿.为完全起见,学校派专车接送教师们上下班.这个接送任务承包给了司机王师傅,正常情况下王师傅用34座的大客车接送教师.由于每次乘车人数不尽相同,为了解教师们的乘车情况,王师傅连续记录了100次的乘车人数,统计结果如下:
乘车人数 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 |
频数 | 2 | 4 | 4 | 10 | 16 | 20 | 16 | 12 | 8 | 6 | 2 |
以这100次记录的各乘车人数的频率作为各乘车人数的概率.
(Ⅰ)若随机抽查两次教师们的乘车情况,求这两次中至少有一次乘车人数超过18的概率;
(Ⅱ)有一次,王师傅的大客车出现了故障,于是王师傅准备租一辆小客车来临时送一次需要乘车的教师.可供选择的小客车只有20座的![]() 型车和22座的
型车和22座的![]() 型车两种,
型车两种, ![]() 型车一次租金为80元,
型车一次租金为80元, ![]() 型车一次租金为90元.若本次乘车教师的人数超过了所租小客车的座位数,王师傅还要付给多出的人每人20元钱供他们乘出租车.以王师傅本次付出的总费用的期望值为依据,判断王师傅租哪种车较合算?
型车一次租金为90元.若本次乘车教师的人数超过了所租小客车的座位数,王师傅还要付给多出的人每人20元钱供他们乘出租车.以王师傅本次付出的总费用的期望值为依据,判断王师傅租哪种车较合算?
【答案】(Ⅰ)0.96.(Ⅱ)租![]() 型车较合算.
型车较合算.
【解析】试题分析:
(Ⅰ)由统计数据可得在一次接送中,乘车人数超过18的概率为0.8,然后根据对立事件和独立事件的概率求解即可得到结论.(Ⅱ)设![]() 表示租用
表示租用![]() 型车的总费用,则
型车的总费用,则![]() 的所有可能取值为80,100,120,140,160,180,结合题意求得相应的概率后可得
的所有可能取值为80,100,120,140,160,180,结合题意求得相应的概率后可得![]() 的分布列,然后求得
的分布列,然后求得![]() ;同样设
;同样设![]() 表示租用
表示租用![]() 型车的总费用,则可得
型车的总费用,则可得![]() ,故租
,故租![]() 型车较合算.
型车较合算.
试题解析:
(Ⅰ)由题意得,在一次接送中,乘车人数超过18的概率为0.8.
记“抽查的两次中至少有一次乘车人数超过18”为事件![]() ,
,
则![]()
![]() .
.
即抽查的两次中至少有一次乘车人数超过18的概率为0.96.
(Ⅱ)设![]() 表示租用
表示租用![]() 型车的总费用(单位:元),则
型车的总费用(单位:元),则![]() 的分布列为
的分布列为
| 80 | 100 | 120 | 140 | 160 | 180 |
| 0.56 | 0.16 | 0.12 | 0.08 | 0.06 | 0.02 |
![]()
![]()
![]()
![]() .
.
设![]() 表示租用
表示租用![]() 型车的总费用(单位:元),则
型车的总费用(单位:元),则![]() 的分布列为
的分布列为
| 90 | 110 | 130 | 150 |
| 0.84 | 0.08 | 0.06 | 0.02 |
![]()
![]() .
.
因此以王师傅本次付出的总费用的期望值为依据,租![]() 型车较合算.
型车较合算.


科目:高中数学 来源: 题型:
【题目】如图,四棱锥P-ABCD的底面为直角梯形,AD∥BC,AD=2BC=2,BC⊥DC,∠BAD=60°,平面PAD⊥底面ABCD,E为AD的中点,△PAD为正三角形,M是棱PC上的一点(异于端点).

(1)若M为PC的中点,求证:PA∥平面BME;
(2)是否存在点M,使二面角MBED的大小为30°.若存在,求出点M的位置;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为 (
(![]() 为参数),将曲线
为参数),将曲线![]() 上各点的横坐标都缩短为原来的
上各点的横坐标都缩短为原来的![]() 倍,纵坐标坐标都伸长为原来的
倍,纵坐标坐标都伸长为原来的![]() 倍,得到曲线
倍,得到曲线![]() ,在极坐标系(与直角坐标系
,在极坐标系(与直角坐标系![]() 取相同的单位长度,且以原点
取相同的单位长度,且以原点![]() 为极点,以
为极点,以![]() 轴非负半轴为极轴)中,直线
轴非负半轴为极轴)中,直线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求直线![]() 和曲线
和曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)设点![]() 是曲线
是曲线![]() 上的一个动点,求它到直线
上的一个动点,求它到直线![]() 的距离的最大值.
的距离的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() (
(![]() ,且
,且![]() ).
).
(Ⅰ)求函数![]() 的单调区间;
的单调区间;
(Ⅱ)求函数![]() 在
在![]() 上的最大值.
上的最大值.
【答案】(Ⅰ)![]() 的单调增区间为
的单调增区间为![]() ,单调减区间为
,单调减区间为![]() .(Ⅱ)当
.(Ⅱ)当![]() 时,
时, ![]()
![]() ;当
;当![]() 时,
时, ![]()
![]() .
.
【解析】【试题分析】(I)利用![]() 的二阶导数来研究求得函数
的二阶导数来研究求得函数![]() 的单调区间.(II) 由(Ⅰ)得
的单调区间.(II) 由(Ⅰ)得![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 上单调递增,由此可知
上单调递增,由此可知![]() .利用导数和对
.利用导数和对![]() 分类讨论求得函数在
分类讨论求得函数在![]() 不同取值时的最大值.
不同取值时的最大值.
【试题解析】
(Ⅰ)![]() ,
,
设![]()
![]() ,则
,则![]() .
.
∵![]() ,
, ![]() ,∴
,∴![]() 在
在![]() 上单调递增,
上单调递增,
从而得![]() 在
在![]() 上单调递增,又∵
上单调递增,又∵![]() ,
,
∴当![]() 时,
时, ![]() ,当
,当![]() 时,
时, ![]() ,
,
因此, ![]() 的单调增区间为
的单调增区间为![]() ,单调减区间为
,单调减区间为![]() .
.
(Ⅱ)由(Ⅰ)得![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 上单调递增,
上单调递增,
由此可知![]() .
.
∵![]() ,
, ![]() ,
,
∴![]() .
.
设![]() ,
,
则![]()
![]()
 .
.
∵当![]() 时,
时, ![]() ,∴
,∴![]() 在
在![]() 上单调递增.
上单调递增.
又∵![]() ,∴当
,∴当![]() 时,
时, ![]() ;当
;当![]() 时,
时, ![]() .
.
①当![]() 时,
时, ![]() ,即
,即![]() ,这时,
,这时, ![]()
![]() ;
;
②当![]() 时,
时, ![]() ,即
,即![]() ,这时,
,这时, ![]()
![]() .
.
综上, ![]() 在
在![]() 上的最大值为:当
上的最大值为:当![]() 时,
时, ![]()
![]() ;
;
当![]() 时,
时, ![]()
![]() .
.
[点睛]本小题主要考查函数的单调性,考查利用导数求最大值. 与函数零点有关的参数范围问题,往往利用导数研究函数的单调区间和极值点,并结合特殊点,从而判断函数的大致图像,讨论其图象与![]() 轴的位置关系,进而确定参数的取值范围;或通过对方程等价变形转化为两个函数图象的交点问题.
轴的位置关系,进而确定参数的取值范围;或通过对方程等价变形转化为两个函数图象的交点问题.
【题型】解答题
【结束】
22
【题目】选修4-4:坐标系与参数方程
在直角坐标系![]() 中,圆
中,圆![]() 的普通方程为
的普通方程为![]() . 在以坐标原点为极点,
. 在以坐标原点为极点,![]() 轴正半轴为极轴的极坐标系中,直线
轴正半轴为极轴的极坐标系中,直线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(Ⅰ) 写出圆 ![]() 的参数方程和直线
的参数方程和直线![]() 的直角坐标方程;
的直角坐标方程;
( Ⅱ ) 设直线![]() 与
与![]() 轴和
轴和![]() 轴的交点分别为
轴的交点分别为![]() ,
,![]() 为圆
为圆![]() 上的任意一点,求
上的任意一点,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() ,命题
,命题![]() 方程
方程![]() 表示焦点在
表示焦点在![]() 轴上的椭圆,命题
轴上的椭圆,命题![]() 方程
方程![]() 表示双曲线.
表示双曲线.
(1)若命题![]() 是真命题,求实数
是真命题,求实数![]() 的范围;
的范围;
(2)若命题“![]() 或
或![]() ”为真命题,“
”为真命题,“![]() 且
且![]() ”是假命题,求实数
”是假命题,求实数![]() 的范围.
的范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】 依法纳税是每个公民应尽的义务,个人取得的所得应依照《中华人民共和国个人所得税法》向国家缴纳个人所得税(简称个税).![]() 年
年![]() 月
月![]() 日起,个税税额根据应纳税所得额、税率和速算扣除数确定,计算公式为:个税税额=应纳税所得额×税率-速算扣除数.①应纳税所得额的计算公式为:应纳税所得额=综合所得收入额-基本减除费用-专项扣除-专项附加扣除-依法确定的其他扣除.②其中,“基本减除费用”(免征额)为每年
日起,个税税额根据应纳税所得额、税率和速算扣除数确定,计算公式为:个税税额=应纳税所得额×税率-速算扣除数.①应纳税所得额的计算公式为:应纳税所得额=综合所得收入额-基本减除费用-专项扣除-专项附加扣除-依法确定的其他扣除.②其中,“基本减除费用”(免征额)为每年![]() 元.税率与速算扣除数见下表.
元.税率与速算扣除数见下表.
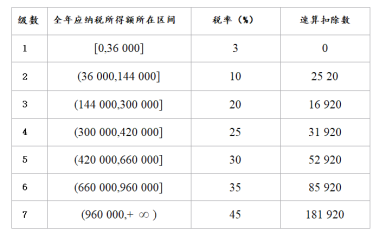
(1)设全年应纳税所得额为![]() ,应缴纳个税税额为
,应缴纳个税税额为![]() ,求
,求![]() 的解析式;
的解析式;
(2)小李全年综合所得收入额为![]() 元,假定缴纳的基本养老保险、基本医疗保险、失业保险等社会保险费和住房公积金占综合所得收入额的比例分别是
元,假定缴纳的基本养老保险、基本医疗保险、失业保险等社会保险费和住房公积金占综合所得收入额的比例分别是![]() ,
,![]() ,
,![]() ,
,![]() ,专项附加扣除是
,专项附加扣除是![]() 元,依法确定其他扣除是
元,依法确定其他扣除是![]() 元,那么他全年应缴纳多少综合所得个税?
元,那么他全年应缴纳多少综合所得个税?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com