
【题目】已知函数![]() (
(![]() 是自然对数的底数,
是自然对数的底数,![]() ).
).
(1)求函数![]() 的图象在
的图象在![]() 处的切线方程;
处的切线方程;
(2)若函数![]() 在区间
在区间![]() 上单调递增,求实数
上单调递增,求实数![]() 的取值范围;
的取值范围;
(3)若函数![]() 在区间
在区间![]() 上有两个极值点
上有两个极值点![]() ,且
,且![]() 恒成立,求满足条件的
恒成立,求满足条件的![]() 的最小值(极值点是指函数取极值时对应的自变量的值).
的最小值(极值点是指函数取极值时对应的自变量的值).
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]() .
.
【解析】
(1)利用导数的几何意义计算即可;
(2)![]() 在
在![]() 上恒成立,只需
上恒成立,只需![]() ,注意到
,注意到![]() ;
;
(3)![]() 在
在![]() 上有两根,令
上有两根,令![]() ,求导可得
,求导可得![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 上单调递增,所以
上单调递增,所以![]() 且
且![]() ,
,![]() ,
,![]() ,求出
,求出![]() 的范围即可.
的范围即可.
(1)因为![]() ,所以
,所以![]() ,
,
当![]() 时,
时,![]() ,
,
所以切线方程为![]() ,即
,即![]() .
.
(2)![]() ,
,![]() .
.
因为函数![]() 在区间
在区间![]() 上单调递增,所以
上单调递增,所以![]() ,且
,且![]() 恒成立,
恒成立,
即![]() ,
,
所以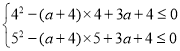 ,即
,即![]() ,又
,又![]() ,
,
故![]() ,所以实数
,所以实数![]() 的取值范围是
的取值范围是![]() .
.
(3)![]() .
.
因为函数![]() 在区间
在区间![]() 上有两个极值点,
上有两个极值点,
所以方程![]() 在
在![]() 上有两不等实根,即
上有两不等实根,即![]() .
.
令![]() ,则
,则![]() ,由
,由![]() ,得
,得![]() ,
,
所以![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 上单调递增,
上单调递增,
所以![]() ,解得
,解得![]() 且
且![]() .
.
又由![]() ,所以
,所以![]() ,
,
且当![]() 和
和![]() 时,
时,![]() 单调递增,
单调递增,
当![]() 时,
时,![]() 单调递减,
单调递减,![]() 是极值点,
是极值点,
此时![]()
令![]() ,则
,则![]() ,
,
所以![]() 在
在![]() 上单调递减,所以
上单调递减,所以![]() .
.
因为![]() 恒成立,所以
恒成立,所以![]() .
.
若![]() ,取
,取![]() ,则
,则![]() ,
,
所以![]() .
.
令![]() ,则
,则![]() ,
,![]() .
.
当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() .
.
所以![]() ,
,
所以![]() 在
在![]() 上单调递增,所以
上单调递增,所以![]() ,
,
即存在![]() 使得
使得![]() ,不合题意.
,不合题意.
满足条件的![]() 的最小值为-4.
的最小值为-4.


科目:高中数学 来源: 题型:
【题目】设椭圆![]() :
:![]() 的左、右焦点分别为
的左、右焦点分别为![]() ,
,![]() ,下顶点为
,下顶点为![]() ,椭圆
,椭圆![]() 的离心率是
的离心率是![]() ,
,![]() 的面积是
的面积是![]() .
.
(1)求椭圆![]() 的标准方程.
的标准方程.
(2)直线![]() 与椭圆
与椭圆![]() 交于
交于![]() ,
,![]() 两点(异于
两点(异于![]() 点),若直线
点),若直线![]() 与直线
与直线![]() 的斜率之和为1,证明:直线
的斜率之和为1,证明:直线![]() 恒过定点,并求出该定点的坐标.
恒过定点,并求出该定点的坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知若椭圆![]() :
:![]() (
(![]() )交
)交![]() 轴于
轴于![]() ,
,![]() 两点,点
两点,点![]() 是椭圆
是椭圆![]() 上异于
上异于![]() ,
,![]() 的任意一点,直线
的任意一点,直线![]() ,
,![]() 分别交
分别交![]() 轴于点
轴于点![]() ,
,![]() ,则
,则![]() 为定值
为定值![]() .
.
(1)若将双曲线与椭圆类比,试写出类比得到的命题;
(2)判定(1)类比得到命题的真假,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】管道清洁棒是通过在管道内释放清洁剂来清洁管道内壁的工具,现欲用清洁棒清洁一个如图1所示的圆管直角弯头的内壁,其纵截面如图2所示,一根长度为![]() 的清洁棒在弯头内恰好处于
的清洁棒在弯头内恰好处于![]() 位置(图中给出的数据是圆管内壁直径大小,
位置(图中给出的数据是圆管内壁直径大小,![]() ).
).
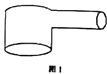

(1)请用角![]() 表示清洁棒的长
表示清洁棒的长![]() ;
;
(2)若想让清洁棒通过该弯头,清洁下一段圆管,求能通过该弯头的清洁棒的最大长度.
查看答案和解析>>
科目:高中数学 来源: 题型:
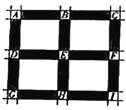
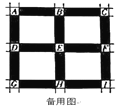
【题目】如图,正方形![]() 是某城市的一个区域的示意图,阴影部分为街道,各相邻的两红绿灯之间的距离相等,
是某城市的一个区域的示意图,阴影部分为街道,各相邻的两红绿灯之间的距离相等,![]() 处为红绿灯路口,红绿灯统一设置如下:先直行绿灯30秒,再左转绿灯30秒,然后是红灯1分钟,右转不受红绿灯影响,这样独立的循环运行.小明上学需沿街道从
处为红绿灯路口,红绿灯统一设置如下:先直行绿灯30秒,再左转绿灯30秒,然后是红灯1分钟,右转不受红绿灯影响,这样独立的循环运行.小明上学需沿街道从![]() 处骑行到
处骑行到![]() 处(不考虑
处(不考虑![]() 处的红绿灯),出发时的两条路线(
处的红绿灯),出发时的两条路线(![]() )等可能选择,且总是走最近路线.
)等可能选择,且总是走最近路线.
(1)请问小明上学的路线有多少种不同可能?
(2)在保证通过红绿灯路口用时最短的前提下,小明优先直行,求小明骑行途中恰好经过![]() 处,且全程不等红绿灯的概率;
处,且全程不等红绿灯的概率;
(3)请你根据每条可能的路线中等红绿灯的次数的均值,为小明设计一条最佳的上学路线,且应尽量避开哪条路线?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程是
的参数方程是 (
(![]() 是参数).以坐标原点
是参数).以坐标原点![]() 为极点,
为极点,![]() 轴的正半轴为极轴建立极坐标系,直线
轴的正半轴为极轴建立极坐标系,直线![]() 的极坐标方程为
的极坐标方程为![]() ,其倾斜角为
,其倾斜角为![]() .
.
(Ⅰ)证明直线![]() 恒过定点
恒过定点![]() ,并写出直线
,并写出直线![]() 的参数方程;
的参数方程;
(Ⅱ)在(Ⅰ)的条件下,若直线![]() 与曲线
与曲线![]() 交于
交于![]() ,
,![]() 两点,求
两点,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]()
(1)若函数![]() 在区间
在区间![]() 上恒成立,求实数a的取值范围;
上恒成立,求实数a的取值范围;
(2)若函数![]() 在区间
在区间![]() 上有两个极值点,求实数a的取值范围;
上有两个极值点,求实数a的取值范围;
(3)若函数![]() 的导函数
的导函数![]() 的图象与函数
的图象与函数![]() 图象有两个不同的交点,求实数a的取值范围.
图象有两个不同的交点,求实数a的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com