
电视传媒为了解某市100万观众对足球节目的收视情况,随机抽取了100名观众进行调查.如图是根据调查结果绘制的观众每周平均收看足球节目时间的频率分布直方图,将每周平均收看足球节目时间不低于1.5小时的观众称为“足球迷”,并将其中每周平均收看足球节目时间不低于2.5小时的观众称为“铁杆足球迷”.
(1)试估算该市“足球迷”的人数,并指出其中“铁杆足球迷”约为多少人;
(2)该市要举办一场足球比赛,已知该市的足球场可容纳10万名观众.根据调查,如果票价定为100元/张,则非“足球迷”均不会到现场观看,而“足球迷”均愿意前往现场观看.如果票价提高 元/张
元/张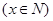 ,则“足球迷”中非“铁杆足球迷”愿意前往观看的人数会减少
,则“足球迷”中非“铁杆足球迷”愿意前往观看的人数会减少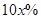 ,“铁杆足球迷”愿意前往观看的人数会减少
,“铁杆足球迷”愿意前往观看的人数会减少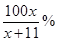 .问票价至少定为多少元/张时,才能使前往现场观看足球比赛的人数不超过10万人?
.问票价至少定为多少元/张时,才能使前往现场观看足球比赛的人数不超过10万人?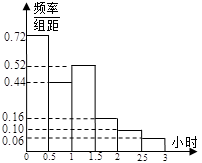
(1)16万“足球迷”, 3万“铁杆足球迷”,(2)140元/张
解析试题分析:(1)利用频数等于频率乘以总数,样本中“足球迷”出现的频率=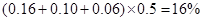 “足球迷”的人数=
“足球迷”的人数= ,同理可求:“铁杆足球迷”=
,同理可求:“铁杆足球迷”= ,(2)如果票价定为100元/张,则非“足球迷”均不会到现场观看,而“足球迷”均愿意前往现场观看,现场观看足球比赛的人数超过10万人,所以设票价为
,(2)如果票价定为100元/张,则非“足球迷”均不会到现场观看,而“足球迷”均愿意前往现场观看,现场观看足球比赛的人数超过10万人,所以设票价为 元,则一般“足球迷”中约有
元,则一般“足球迷”中约有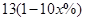 万人,“铁杆足球迷”约有
万人,“铁杆足球迷”约有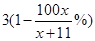 万人去现场看球. 由
万人去现场看球. 由 得
得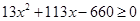 由
由 ,
,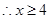 即平均票价至少定为100+40=140元,才能使前往现场观看足球比赛的“足球迷”不超过10万人.
即平均票价至少定为100+40=140元,才能使前往现场观看足球比赛的“足球迷”不超过10万人.
解:
(1)样本中“足球迷”出现的频率= (2分)
(2分)
“足球迷”的人数= (万) (4分)
(万) (4分)
“铁杆足球迷”= (万)
(万)
所以16万“足球迷”中,“铁杆足球迷”约有3万人. (6分)
(2)设票价为 元,则一般“足球迷”中约有
元,则一般“足球迷”中约有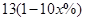 万人,“铁杆足球迷”约有
万人,“铁杆足球迷”约有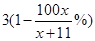 万人去现场看球. (3分)
万人去现场看球. (3分)
令 (5分)
(5分)
化简得: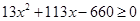
解得: ,由
,由 ,
,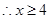 (7分)
(7分)
即平均票价至少定为100+40=140元,才能使前往现场观看足球比赛的“足球迷”不超过10万人. (8分)
考点:频率分布直方图


科目:高中数学 来源: 题型:解答题
下表是某种产品销售收入与销售量之间的一组数据:
| 销售量x(吨) | 2 | 3 | 5 | 6 |
| 销售收入y(千元) | 7 | 8 | 9 | 12 |
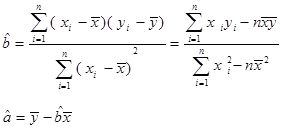
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本小题满分12分)
海关对同时从 三个不同地区进口的某种商品进行抽样检测,从各地区进口此种商品的数量(单位:件)如右表所示,工作人员用分层抽样的方法从这些商品中共抽取6件进行检测
三个不同地区进口的某种商品进行抽样检测,从各地区进口此种商品的数量(单位:件)如右表所示,工作人员用分层抽样的方法从这些商品中共抽取6件进行检测
| 地区 |  |  |  |
| 数量 | 50 | 150 | 100 |
 各地区商品的数量;
各地区商品的数量;查看答案和解析>>
科目:高中数学 来源: 题型:解答题
20名学生某次数学考试成绩(单位:分)的频数分布直方图如下:
(1)求频率分布直方图中 的值;
的值;
(2)分别球出成绩落在 与
与 中的学生人数;
中的学生人数;
(3)从成绩在 的学生中人选2人,求此2人的成绩都在
的学生中人选2人,求此2人的成绩都在 中的概率.
中的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
从一批苹果中,随机抽取50个,其重量(单位:g)的频数分布表如下:
| 分组(重量) | [80,85) | [85,90) | [90,95) | [95,100) |
| 频数(个) | 5 | 10 | 20 | 15 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某中学一位高三班主任对本班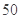 名学生学习积极性和对待班级工作的态度进行长期的调查,得到的统计数据如下表所示:
名学生学习积极性和对待班级工作的态度进行长期的调查,得到的统计数据如下表所示:
| | 积极参加班级工作 | 不太主动参加班级工作 | 合计 |
| 学习积极性高 | 18 | 7 | 25 |
| 学习积极性一般 | 6 | 19 | 25 |
| 合计 | 24 | 26 | 50 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
下表是某市从3月份中随机抽取的 天空气质量指数(
天空气质量指数( )和“
)和“ ”(直径小于等于
”(直径小于等于 微米的颗粒物)
微米的颗粒物) 小时平均浓度的数据,空气质量指数(
小时平均浓度的数据,空气质量指数( )小于
)小于 表示空气质量优良.
表示空气质量优良.
| 日期编号 |  |  |  |  |  |  |  |  |  |  |
空气质量指数( ) ) |  |  |  |  |  |  |  |  |  |  |
“ ” ” 小时平均浓度( 小时平均浓度( ) ) |  |  |  |  |  |  |  |  |  |  |
 为“抽取的两个日期中,当天‘
为“抽取的两个日期中,当天‘ ’的
’的 小时平均浓度不超过
小时平均浓度不超过 ”,求事件
”,求事件 发生的概率;
发生的概率; 天,记
天,记 为“
为“ ”
” 小时平均浓度不超过
小时平均浓度不超过 的天数,求
的天数,求 的分布列和数学期望.
的分布列和数学期望.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
在数学趣味知识培训活动中,甲、乙两名学生的5次培训成绩如下茎叶图所示: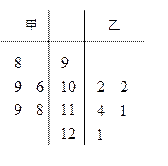
(1)从甲、乙两人中选择1人参加数学趣味知识竞赛,你会选哪位?请运用统计学的知识说明理由;
(2) 从乙的5次培训成绩中随机选择2个,试求选到121分的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
一个盒子中装有大量形状大小一样但重量不尽相同的小球,从中随机抽取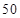 个作为样本,称出它们的重量(单位:克),重量分组区间为
个作为样本,称出它们的重量(单位:克),重量分组区间为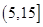 ,
,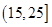 ,
,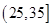 ,
, ,由此得到样本的重量频率分布直方图,如图
,由此得到样本的重量频率分布直方图,如图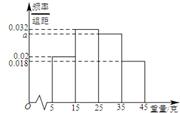
(1)求 的值;
的值;
(2)根据样本数据,试估计盒子中小球重量的平均值;
(注:设样本数据第 组的频率为
组的频率为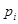 ,第
,第 组区间的中点值为
组区间的中点值为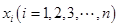 ,则样本数据的平均值为
,则样本数据的平均值为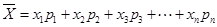 .)
.)
(3)从盒子中随机抽取 个小球,其中重量在
个小球,其中重量在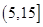 内的小球个数为
内的小球个数为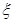 ,求
,求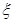 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com