
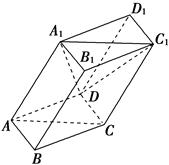
 .(3)存在,点P在C1C的延长线上且使C1C=CP.
.(3)存在,点P在C1C的延长线上且使C1C=CP.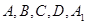 的坐标,进而得
的坐标,进而得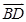 ,
, 坐标,由坐标运算可得
坐标,由坐标运算可得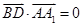 ,即两向量垂直,得两线垂直;(2)分别求出两平面的一个法向量
,即两向量垂直,得两线垂直;(2)分别求出两平面的一个法向量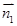 ,
,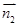 ,利用
,利用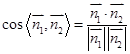 ,可得二面角的平面角的余弦值;(3)令存在,在直线CC1 上设
,可得二面角的平面角的余弦值;(3)令存在,在直线CC1 上设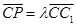 ,P(x,y,z),得
,P(x,y,z),得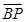 =(
=( ,1+λ,
,1+λ, λ),取平面DA1C一法向量
λ),取平面DA1C一法向量 ,知
,知 ·
·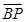 =0,得
=0,得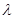 的值,P点可求.
的值,P点可求.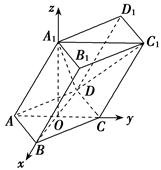
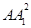 +AO2-2AA1·AOcos 60°=3,
+AO2-2AA1·AOcos 60°=3, ,0,0),C(0,1,0),D(
,0,0),C(0,1,0),D( ,0,0),A1(0,0,
,0,0),A1(0,0, ).
).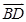 =(
=(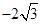 ,0,0),
,0,0), =(0,1,
=(0,1, ),则
),则 ·
·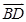 =0×(
=0×(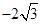 )+1×0+
)+1×0+ ×0=0,
×0=0,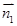 =(1,0,0),设
=(1,0,0),设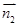 ⊥平面AA1D,则
⊥平面AA1D,则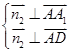
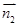 =(x,y,z),
=(x,y,z),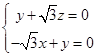 取
取 , 6分
, 6分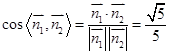 ,
,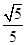 . 8分
. 8分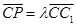 ,P(x,y,z),则(x,y-1,z)=λ(0,1,
,P(x,y,z),则(x,y-1,z)=λ(0,1, ), 9分
), 9分 λ),
λ),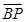 =(
=( ,1+λ,
,1+λ, λ).
λ). ⊥平面DA1C1,则
⊥平面DA1C1,则 .
. =(x3,y3,z3),得到
=(x3,y3,z3),得到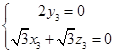 .
. =(1,0,-1). 10分
=(1,0,-1). 10分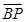 ∥平面DA1C1,则
∥平面DA1C1,则 ·
·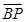 =0,即
=0,即 -
- λ=0,得λ=-1,
λ=0,得λ=-1,

科目:高中数学 来源:不详 题型:解答题
 的正方形
的正方形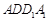 中,点
中,点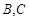 在线段
在线段 上,且
上,且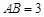 ,
,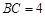 ,作
,作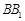 //
//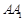 ,分别交
,分别交 ,
,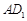 于点
于点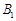 ,
,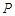 ,作
,作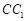 //
//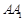 ,分别交
,分别交 ,
,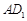 于点
于点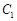 ,
,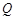 ,将该正方形沿
,将该正方形沿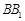 ,
,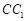 折叠,使得
折叠,使得 与
与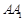 重合,构成如图所示的三棱柱
重合,构成如图所示的三棱柱 .
.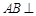 平面
平面 ;
; 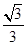 ,求|BE|的最小值.
,求|BE|的最小值.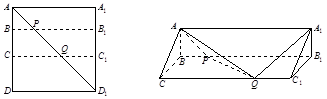
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
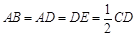 ,M是线段AE上的动点.
,M是线段AE上的动点.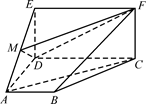
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
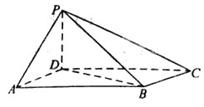
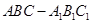 所有棱长都是2,D棱AC的中点,E是
所有棱长都是2,D棱AC的中点,E是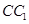 棱的中点,AE交
棱的中点,AE交 于点H.
于点H.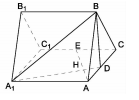
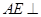 平面
平面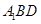 ;
;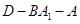 的余弦值;
的余弦值;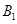 到平面
到平面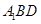 的距离.
的距离.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com