
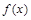 在
在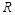 上有定义,对任意实数
上有定义,对任意实数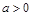 和任意实数
和任意实数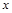 ,都有
,都有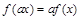 .
. 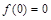 ;
;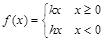 (其中k和h均为常数);
(其中k和h均为常数);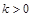 的时,设
的时,设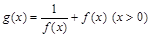 ,讨论
,讨论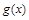 在
在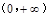 内的单调性.
内的单调性.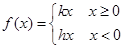
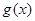 在区间
在区间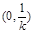 内单调递减, 在区间(
内单调递减, 在区间(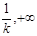 )内单调递增.
)内单调递增.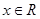 ,均有
,均有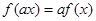 ①在①中取
①在①中取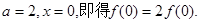
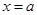 时,∵
时,∵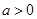 ,∴
,∴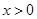 ,则
,则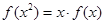
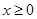 时,
时,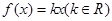 ,则
,则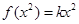
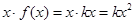 , ∴
, ∴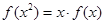 ,即
,即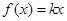 成立
成立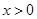 时,
时,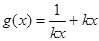 ,
,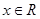 ,均有
,均有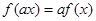 ①
①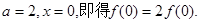
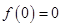 ②
②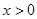 时,由①得
时,由①得 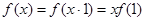
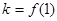 ,则有
,则有 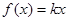 ③
③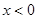 时,由①得
时,由①得 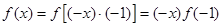
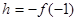 ,则有
,则有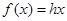 ④
④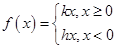 ;
;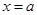 时,∵
时,∵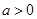 ,∴
,∴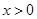 ,则
,则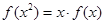
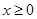 时,
时,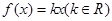 ,则
,则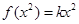
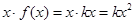 , ∴
, ∴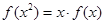 ,即
,即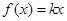 成立
成立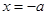 ,∵
,∵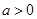 ,∴
,∴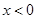 ,则
,则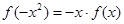
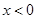 时,
时,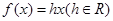 ,则
,则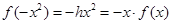
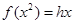 成立。综上知
成立。综上知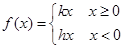
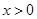 时,
时,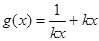 ,
,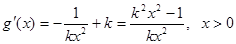
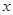 | 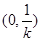 | 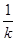 | 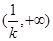 |
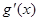 | - | 0 | + |
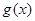 | ↘ | 极小值2 | ↗ |
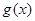 在区间
在区间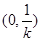 内单调递减,在区间(
内单调递减,在区间(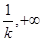 )内单调递增。
)内单调递增。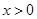 时,
时,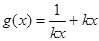 ,
,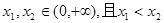 则
则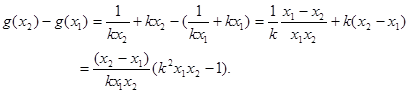
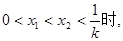
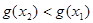 ;
;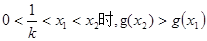
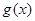 在区间
在区间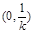 内单调递减, 在区间(
内单调递减, 在区间(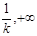 )内单调递增.
)内单调递增.

湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com