练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    函数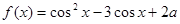 的最大值为6.求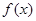最小值.

    a=1，最小值为0 。

    解析试题分析：令 则可化为，而函数 的最大值为6.即t=-1时，1-3+2a=6，所以a=1.当t=1时，最小值为0.
    考点：本题主要考查二次函数的图象和性质，余弦函数的值域（有界性）。
    点评：小综合题，利用换元法，将问题转化成二次函数闭区间上的最值问题。本题比较基础、典型。

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：解答题

    已知函数
    （1）求函数的定义域；
    （2）若存在,对任意，总存在唯一，使得成立.求实数的取值范围.

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    欲修建一横断面为等腰梯形(如图1)的水渠，为降低成本必须尽量减少水与渠壁的接触面，若水渠横断面面积设计为定值S，渠深h，则水渠壁的倾角α(0°<α<90°)应为多大时，方能使修建成本最低?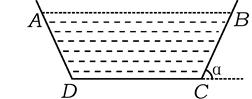

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    已知函数f（x）＝log2（x＋m），且f（0）、f（2）、f（6）成等差数列．
    （1）求实数m的值；
    （2）若a、b、c是两两不相等的正数，且a、b、c成等比数列，试判断f（a）＋f(c)与2f(b)的大小关系，并证明你的结论．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    计算：
    （1）          
    （2）

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    已知函数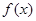是定义在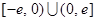上的奇函数，当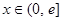时，有（其中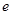为自然对数的底，）．
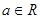    （1）求函数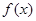的解析式；
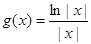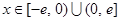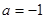    （2）设，，求证：当时，；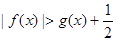
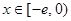    （3）试问：是否存在实数，使得当时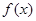，的最小值是3？如果存在，求出实数的值；如果不存在，请说明理由．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

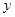    某商品的进价为每件40元，售价为每件50元，每个月可卖出210件；如果每件商品在该售价的基础上每上涨1元，则每个月少卖10件（每件售价不能高于65元）．设每件商品的售价上涨元（为正整数），每个月的销售利润为元．(14分)
    （1）求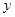与的函数关系式并直接写出自变量的取值范围；
    （2）每件商品的售价定为多少元时，每个月可获得最大利润？最大的月利润是多少元？

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    已知幂函数为偶函数，且在区间上是单调减函数（Ⅰ）求函数；（Ⅱ）讨论的奇偶性.

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    （本题满分13分）某工厂有214名工人, 现要生产1500件产品, 每件产品由3个A型零件与1个B型零件配套组成, 每个工人加工5个A型零件与3个B型零件所需时间相同. 现将全部工人分为两组, 分别加工一种零件, 同时开始加工. 设加工A型零件的工人有x人, 在单位时间内每人加工A型零件5k个(k∈N*), 加工完A型零件所需时间为g(x), 加工完B型零件所需时间为h (x).
     (Ⅰ) 试比较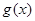与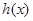大小, 并写出完成总任务的时间的表达式；
    (Ⅱ) 怎样分组才能使完成任务所需时间最少?

    查看答案和解析>>

    同步练习册答案