
【题目】某工厂甲、乙两个车间包装同一种产品,在自动包装传送带上每隔一小时抽一包产品,称其重量(单位:克)是否合格,分别记录抽查数据,获得重量数据茎叶如图所示.
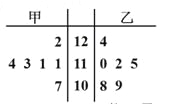
(Ⅰ)根据样本数据,计算甲、乙两个车间产品重量的均值与方差,并说明哪个车间的产品的重量相对稳定;
(Ⅱ)若从乙车间![]() 件样品中随机抽取两件,求所抽取两件样品重量之差不超过
件样品中随机抽取两件,求所抽取两件样品重量之差不超过![]() 克的概率.
克的概率.
【答案】(1)甲车间的产品的重量相对较稳定. (2)![]() .
.
【解析】试题分析:(1)根据茎叶图所给的两组数据,分别做出这两组数据的平均数,再作出这两组数据的方差,得到甲车间的产品的重量相对较稳定;(2)由题意知本题是一个古典概型的概率,试验发生包含的事件数,可以通过列举得到共有15种结果,而满足条件的事件数也通过列举得到,两个做比值得到概率
试题解析:(1)设甲、乙两个车间产品重量的均值分别为![]() 、
、![]() ,方差分别为
,方差分别为![]() 、
、![]() ,
,
则![]()
![]() .
.
![]() .
.
![]() .
.
由于![]() ,所以甲车间的产品的重量相对稳定.
,所以甲车间的产品的重量相对稳定.
(2)设“所抽取两件样品重量之差不超过![]() 克”为事件
克”为事件![]() .
.
总的基本事件有![]() 个:
个:![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() ,它们是等可能的
,它们是等可能的
事件![]() 包含的基本事件有
包含的基本事件有![]() 个:
个:![]() 、
、![]() 、
、![]() 、
、![]()
所以![]()
答:甲车间的产品的重量相对稳定;从乙车间![]() 件样品中随机抽取两件,所抽取两件样品重量之差不超过
件样品中随机抽取两件,所抽取两件样品重量之差不超过![]() 克的概率为
克的概率为![]()


 出彩同步大试卷系列答案
出彩同步大试卷系列答案科目:高中数学 来源: 题型:
【题目】为美化校园,江苏省淮阴中学将一个半圆形的边角地改造为花园.如图所示,O为圆心,半径为1千米,点A、B、P都在半圆弧上,设∠NOP=∠POA=![]() ,∠AOB=
,∠AOB=![]() ,且
,且![]() .
.
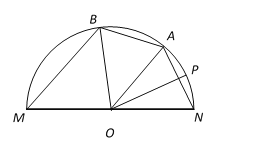
(1)请用![]() 分别表示线段NA、BM的长度;
分别表示线段NA、BM的长度;
(2)若在花园内铺设一条参观线路,由线段NA、AB、BM三部分组成,则当![]() 取何值时,参观线路最长?
取何值时,参观线路最长?
(3)若在花园内的扇形ONP和四边形OMBA内种满杜鹃花,则当![]() 取何值时,杜鹃花的种植总面积最大?
取何值时,杜鹃花的种植总面积最大?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】过椭圆![]() 的左顶点
的左顶点![]() 作斜率为2的直线,与椭圆的另一个交点为
作斜率为2的直线,与椭圆的另一个交点为![]() ,与
,与![]() 轴的交点为
轴的交点为![]() ,已知
,已知![]() .
.
(1)求椭圆的离心率;
(2)设动直线![]() 与椭圆有且只有一个公共点
与椭圆有且只有一个公共点![]() ,且与直线
,且与直线![]() 相交于点
相交于点![]() ,若
,若![]() 轴上存在一定点
轴上存在一定点![]() ,使得
,使得![]() ,求椭圆的方程.
,求椭圆的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() ,函数
,函数![]() .
.
(1)求实数![]() 的值,使得
的值,使得![]() 为奇函数;
为奇函数;
(2)若关于![]() 的方程
的方程![]() 有两个不同实数解,求
有两个不同实数解,求![]() 的取值范围;
的取值范围;
(3)若关于![]() 的不等式
的不等式![]() 对任意
对任意![]() 恒成立,求
恒成立,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对由![]() 和
和![]() 这两个数字组成的字符串,作如下规定:按从左向右的顺序,当第一个子串“
这两个数字组成的字符串,作如下规定:按从左向右的顺序,当第一个子串“![]() ”的最后一个
”的最后一个![]() 所在数位是第
所在数位是第![]() (
(![]() ,且
,且![]() )位,则称子串“
)位,则称子串“![]() ”在第
”在第![]() 位出现;再继续从第
位出现;再继续从第![]() 位按从左往右的顺序找子串“
位按从左往右的顺序找子串“![]() ”,若第二个子串“
”,若第二个子串“![]() ”的最后一个
”的最后一个![]() 所在数位是第
所在数位是第![]() 位(其中
位(其中![]() 且
且![]() ),则称子串“
),则称子串“![]() ”在第
”在第![]() 位出现;……;如此不断地重复下去.如:在字符串
位出现;……;如此不断地重复下去.如:在字符串![]() 中,子串“
中,子串“![]() ”在第
”在第![]() 位和第
位和第![]() 位出现,而不是在第
位出现,而不是在第![]() 位和第
位和第![]() 位出现.记在
位出现.记在![]() 位由
位由![]() 组成的所有字符串中,子串“
组成的所有字符串中,子串“![]() ”在第
”在第![]() 位出现的字符串的个数为
位出现的字符串的个数为![]() .
.
(1)求![]() 的值;
的值;
(2)求证:对任意的正整数![]() ,
,![]() 是
是![]() 的倍数.
的倍数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】经销商经销某种农产品,在一个销售季度内,每售出1t该产品获利润500元,未售出的产品,每1t亏损300元.根据历史资料,得到销售季度内市场需求量的频率分布直方图,如右图所示.经销商为下一个销售季度购进了130t该农产品.以x(单位:t,100≤x≤150)表示下一个销售季度内经销该农产品的数量,T表示利润.
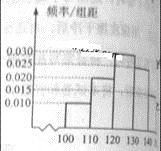
(Ⅰ)将T表示为x的函数
(Ⅱ)根据直方图估计利润T不少于57000元的概率;
(Ⅲ)在直方图的需求量分组中,以各组的区间中点值代表该组的各个值需求量落入该区间的频率作为需求量取该区间中点值的概率(例如:若x![]() ,则取x=105,且x=105的概率等于需求量落入[100,110
,则取x=105,且x=105的概率等于需求量落入[100,110![]() ,求T的数学期望.
,求T的数学期望.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com