解:(1)F(x)=

,(1分)
令log
2(x
2+1)≥log
2(|x|+7),得x
2-|x|-6≥0,(3分)
解得:x≤-3或x≥3,(5分)∴F(x)=

.(8分)
(写出

4分)
(2)当x≥3或x≤-3时,F(x)=log
2(x
2+1),设u=x
2+1≥10,y=log
2u在[10,+∞)上递增,所以F(x)
min=log
210(10分);(说明:设元及单调性省略不扣分)
同理,当-3<x<3,F(x)
min=log
27;(12分)
又log
27<log
210∴x∈R时,F(x)
min=log
27.(14分)
或解:因为F(x)是偶函数,所以只需要考虑x≥0的情形,(9分)
当0≤x<3,F(x)=log
2(x
2+7),当x=0时,F(x)
min=log
27;(11分)
当x≥3时,F(x)=log
2(x
2+1),当x=3时,F(x)
min=log
210;(12分)∴x∈R时,F(x)
min=log
27.(14分)
分析:(1)令log
2(x
2+1)≥log
2(|x|+7),解得:x的取值范围,再结合F(x)的意义用分段函数形式写出函数F(x)的解析式即可;
(2)先分情况讨论函数的单调性:当x≥3或x≤-3时;当-3<x<3,分别求出F(x)的最小值,最后综合得出x∈R时,F(x)
min=log
27.
或利用F(x)的奇偶性,只需要考虑x≥0的情形,只须分两种情形讨论:当0≤x<3,当x≥3时,分别求得F(x)的最小值即得.
点评:本小题主要考查函数单调性的应用、函数解析式的求解及常用方法、不等式的解法等基础知识,考查运算求解能力,考查分类讨论思想、化归与转化思想.属于基础题.

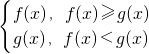 ,其中f(x)=log2(x2+1),g(x)=log2(|x|+7).
,其中f(x)=log2(x2+1),g(x)=log2(|x|+7). ,(1分)
,(1分) .(8分)
.(8分) 4分)
4分)
