
已知向量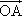 =a,
=a,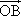 =b,∠AOB=60°,且|a|=|b|=4.
=b,∠AOB=60°,且|a|=|b|=4.
(1)求|a+b|,|a-b|;
(2)求a+b与a的夹角及a-b与a的夹角.
|
解法一: (1)|a+b|2=(a+b)2=a2+2a·b+b2=|a|2+2|a||b|cos60°+|b|2=42+2×4×4cos60°+42=16+16+16=48,∴|a+b|=43. |a-b|2=(a-b)2=a2-2a·b+b2=|a|2-2|a||b|cos60°+|b|2=42-2×4×4cos60°+42=16-16+16=16,∴|a-b|=4. (2)记a+b与a的夹角为α,a-b与a的夹角为β,则 cosα= cosβ= ∴α=60°. 解法二:如图,以OA,OB为邻边作平行四边形OACB.
∵|a|=|b|=4,∴四边形OACB为菱形.
|


 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案科目:高中数学 来源:成功之路·突破重点线·数学(学生用书) 题型:013
已知a、b为非零向量,且a=(x1,y1),b=(x2,y2),则下列命题中与a⊥b等价的个数有
①a·b=0;②x1x2+y1y2=0;③|a+b|2=|a-b|2;④a2+b2=(a-b)2
[ ]
查看答案和解析>>
科目:高中数学 来源:学习周报 数学 北师大课标高一版(必修4) 2009-2010学年 第46期 总202期 北师大课标版 题型:013
e1,e2为基底向量,已知向量![]() =e1-ke2,
=e1-ke2,![]() =2e1+e2,
=2e1+e2,![]() =3e1-e2,若A,B,D三点共线,则k的值为
=3e1-e2,若A,B,D三点共线,则k的值为
2
-3
-2
3
查看答案和解析>>
科目:高中数学 来源:山西省山大附中2012届高三4月月考数学文科试题 题型:013
已知向量![]() =(x-z,1),
=(x-z,1),![]() =(2,y+z),且
=(2,y+z),且![]() ⊥
⊥![]() ,若变量x,y满足约束条件
,若变量x,y满足约束条件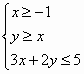 则z的最大值为
则z的最大值为
A.1
B.2
C.3
D.4
查看答案和解析>>
科目:高中数学 来源:2013届四川省高二下学期期中考试理科数学试卷(解析版) 题型:选择题
已知向量 =(1,1,0),
=(1,1,0), =(-1, 0,2),且
=(-1, 0,2),且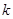
 +
+ 与2
与2 -
- 互相垂直,则
互相垂直,则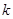 的值是( )
的值是( )
A.1
B. C.
C. D.
D.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com