设M为部分正整数组成的集合,数列{an}的首项a1=1,前n项和为Sn,已知对任意整数k∈M,当整数n>k时,Sn+k+Sn-k=2(Sn+Sk)都成立
(1)设M={1},a2=2,求a5的值;
(2)设M={3,4},求数列{an}的通项公式.
分析:(1)由集合M的元素只有一个1,得到k=1,所以当n大于1即n大于等于2时,Sn+1+Sn-1=2(Sn+S1)都成立,变形后,利用Sn+1-Sn=an+1,及a1=1化简,得到当n大于等于2时,此数列除去首项后为一个等差数列,根据第2项的值和确定出的等差写出等差数列的通项公式,因为5大于2,所以把n=5代入通项公式即可求出第5项的值;
(2)当n大于k时,根据题意可得Sn+k+Sn-k=2(Sn+Sk),记作①,把n换为n+1,得到一个关系式记作②,②-①后,移项变形后,又k等于3或4得到当n大于等于8时此数列每隔3项或4项成等差数列,即an-6,an-3,an,an+3,an+6成等差数列,根据等差数列的性质得到一个关系式,记作(*),且an-6,an-2,an+2,an+6也成等差数列,又根据等差数列的性质得到另外一个关系式,等量代换得到an+2-an=an-an-2,得到当n大于等于9时,每隔两项成等差数列,设出等差数列的四项,根据等差数列的性质化简变形,设d=an-an-1,从而得到当n大于等于2小于等于8时,n+6大于等于8,把n+6代入(*)中,得到一个关系式,同时把n+7也代入(*)得到另外一个关系式,两者相减后根据设出的d=an-an-1,经过计算后,得到n大于等于2时,d=an-an-1都成立,从而把k=3和k=4代入到已知的等式中,化简后得到d与前3项的和及d与前4项和的关系式,两关系式相减即可表示出第4项的值,根据d=an-an-1,同理表示出第3项,第2项及第1项,得到此数列为等差数列,由首项等于1即可求出d的值,根据首项和等差写出数列的通项公式即可.
解答:解:(1)由M={1},根据题意可知k=1,所以n≥2时,S
n+1+S
n-1=2(S
n+S
1),
即(S
n+1-S
n)-(S
n-S
n-1)=2S
1,又a
1=1,
则a
n+1-a
n=2a
1=2,又a
2=2,
所以数列{a
n}除去首项后,是以2为首项,2为公差的等差数列,
故当n≥2时,a
n=a
2+2(n-2)=2n-2,
所以a
5=8;
(2)根据题意可知当k∈M={3,4},
且n>k时,S
n+k+S
n-k=2(S
n+S
k)①,且S
n+1+k+S
n+1-k=2(S
n+1+S
k)②,
②-①得:(S
n+1+k-S
n+k)+(S
n+1-k-S
n-k)=2(S
n+1-S
n),
即a
n+1+k+a
n+1-k=2a
n+1,可化为:a
n+1+k-a
n+1=a
n+1-a
n+1-k所以n≥8时,a
n-6,a
n-3,a
n,a
n+3,a
n+6成等差数列,且a
n-6,a
n-2,a
n+2,a
n+6也成等差数列,
从而当n≥8时,2a
n=a
n-3+a
n+3=a
n-6+a
n+6,(*)且a
n-2+a
n+2=a
n-6+a
n+6,
所以当n≥8时,2a
n=a
n-2+a
n+2,即a
n+2-a
n=a
n-a
n-2,
于是得到当n≥9时,a
n-3,a
n-1,a
n+1,a
n+3成等差数列,从而a
n-3+a
n+3=a
n-1+a
n+1,
由(*)式可知:2a
n=a
n-1+a
n+1,即a
n+1-a
n=a
n-a
n-1,
当n≥9时,设d=a
n-a
n-1,
则当2≤n≤8时,得到n+6≥8,从而由(*)可知,2a
n+6=a
n+a
n+12,得到2a
n+7=a
n+1+a
n+13,
两式相减得:2(a
n+7-a
n+6)=a
n+1-a
n+(a
n+13-a
n+12),
则a
n+1-a
n=2d-d=d,
因此,a
n-a
n-1=d对任意n≥2都成立,
又由S
n+k+S
n-k-2S
n=2S
k,可化为:(S
n+k-S
n)-(S
n-S
n-k)=2S
k,
当k=3时,(S
n+3-S
n)-(S
n-S
n-3)=9d=2S
3;同理当k=4时,得到16d=2S
4,
两式相减得:2(S
4-S
3)=2a
4=16d-9d=7d,解得a
4=
d,
因为a
4-a
3=d,解得a
3=
d,同理a
2=
d,a
1=
,
则数列{a
n}为等差数列,由a
1=1可知d=2,
所以数列{a
n}的通项公式为a
n=1+2(n-1)=2n-1.
点评:此题考查学生灵活运用数列的递推式化简求值,掌握确定数列为等差数列的方法,会根据等差数列的首项和等差写出数列的通项公式,是一道中档题.



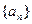 的首项
的首项 ,前n项和为
,前n项和为 ,已知对任意整数k属于M,当n>k时,
,已知对任意整数k属于M,当n>k时, 都成立。
都成立。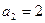 ,求
,求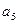 的值;(2)设M={3,4},求数列
的值;(2)设M={3,4},求数列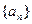 的通项公式。
的通项公式。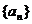 的首项
的首项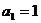 ,前n项和为
,前n项和为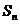 ,已知对任意整数k属于M,当n>k时,
,已知对任意整数k属于M,当n>k时,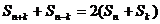 都成立。
都成立。 ,求
,求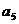 的值;(2)设M={3,4},求数列
的值;(2)设M={3,4},求数列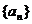 的通项公式。
的通项公式。