设有关于x的一元二次方程x2+2ax+b2=0.
(Ⅰ)若a是从0,1,2,3四个数中任取的一个数,b是从0,1,2三个数中任取的一个数,记方程有两不等实根为事件A,方程没有实数根记为事件B,求事件A+B的概率
(Ⅱ)若a是从区间[0,3]任取的一个数,b是从区间[0,2]任取的一个数,求上述方程有实根的概率.
【答案】
分析:(1)本题是一个古典概型,由分步计数原理知基本事件共12个,方程x
2+2ax+b
2=0有实根的充要条件为a>b,满足条件的事件中包含6个基本事件,由古典概型公式得到事件A发生的概率,同理可得出事件B发生的概率,最后利用互斥事件的加法公式即可求出结果.
(2)本题是一个几何概型,试验的全部约束所构成的区域为{(a,b)|0≤a≤3,0≤b≤2}.构成事件A的区域为{(a,b)|0≤a≤3,0≤b≤2,a≥b}.根据几何概型公式得到结果.
解答:解:(Ⅰ)由题意可知,总的基本事件有:
(0,0)、(0,1)、(0,2)、(1,0)、(1,1)、(1,2)、
(2,0)、(2,1)、(2,2)、(3,0)、(3,1)、(3,2)共有12个…(1分)
事件A发生,要求△=4a
2-4b
2>0,即a
2>b
2,
符合的基本事件有(1,0)、(2,0)、
(2,1)、(3,0)、(3,1)、(3,2),共6个…(2分)
故P(A)=
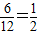
…(3分)
事件B发生要求△=4a
2-4b
2<0,即a
2<b
2,符合的基本事件有:(0,1)、(0,2)、
(1,2)共3个…(4分)
故P(B)=
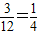
…(5分)
又事件A、B互斥,
∴P(A+B)=P(A)+P(B)=

…(6分)
(Ⅱ)试验的全部约束所构成的区域为{(a,b)|0≤a≤3,0≤b≤2}.
构成事件A的区域为{(a,b)|0≤a≤3,0≤b≤2,a≥b}.
所以所求的概率为=
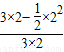
=

…(12分)
点评:本题考查几何概型和古典概型,放在一起的目的是把两种概型加以比较,几何概型和古典概型是高中必修中学习的高考时常以选择和填空出现,有时文科会考这种类型的解答题.

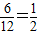 …(3分)
…(3分)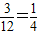 …(5分)
…(5分) …(6分)
…(6分)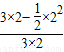 =
= …(12分)
…(12分)

 中考解读考点精练系列答案
中考解读考点精练系列答案