
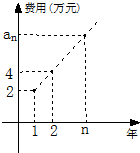
 某公司今年初用25万元引进一种新的设备,设备投入运行后,每年销售收入为21万元.已知该公司第n年需要付出设备的维修和工人工资等费用的和an的信息如图.
某公司今年初用25万元引进一种新的设备,设备投入运行后,每年销售收入为21万元.已知该公司第n年需要付出设备的维修和工人工资等费用的和an的信息如图.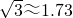 )
)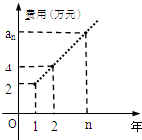 解:(1)由题意知,每年的费用是以2为首项,2为公差的
解:(1)由题意知,每年的费用是以2为首项,2为公差的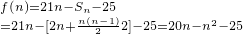 …(5分)
…(5分) …(6分)
…(6分)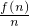 =20-
=20- …(10分)
…(10分)

科目:高中数学 来源: 题型:解答题
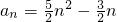 (n∈N*),求:数列{△an}的通项公式;
(n∈N*),求:数列{△an}的通项公式;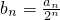 ,求证:数列{bn}是等差数列,并求数列{bn}的通项公式;
,求证:数列{bn}是等差数列,并求数列{bn}的通项公式;查看答案和解析>>
科目:高中数学 来源: 题型:解答题
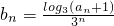 ,且Tn=b1+b2+…+bn,求Tn;
,且Tn=b1+b2+…+bn,求Tn;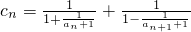 ,数列{cn}的前n项和为Mn,求证:
,数列{cn}的前n项和为Mn,求证: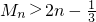 .
.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:单选题
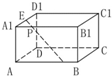 如图,在长方体ABCD-A1B1C1D1中,AA1=1,点E、F分别在棱A1D1,AB上,且线段EF的长恒等于2,则EF的中点P的轨迹是
如图,在长方体ABCD-A1B1C1D1中,AA1=1,点E、F分别在棱A1D1,AB上,且线段EF的长恒等于2,则EF的中点P的轨迹是查看答案和解析>>
科目:高中数学 来源: 题型:解答题
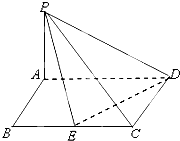 如图,四边形ABCD为矩形,且AD=2,AB=1,PA⊥平面ABCD,PA=1,E为BC的中点.
如图,四边形ABCD为矩形,且AD=2,AB=1,PA⊥平面ABCD,PA=1,E为BC的中点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com