
(本小题满分12)
为了绿化城市,准备在如图所示的区域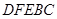 内修建一个矩形
内修建一个矩形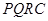 的草坪,并建立如图平面直角坐标系,且
的草坪,并建立如图平面直角坐标系,且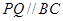 ,
,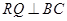 ,另外
,另外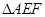 的内部有一文物保护区不能占用,经测量
的内部有一文物保护区不能占用,经测量 ,
,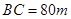 ,
, 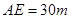 ,
,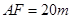 .
.
(1)求直线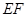 的方程;
的方程;
(2)应如何设计才能使草坪的占地面积最大?并求最大面积。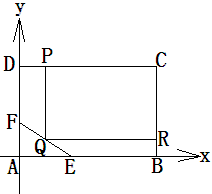
科目:高中数学 来源: 题型:解答题
(本小题满分14分)
已知函数f (x)=ex,g(x)=lnx,h(x)=kx+b.
(1)当b=0时,若对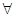 x∈(0,+∞)均有f (x)≥h(x)≥g(x)成立,求实数k的取值范围;
x∈(0,+∞)均有f (x)≥h(x)≥g(x)成立,求实数k的取值范围;
(2)设h(x)的图象为函数f (x)和g(x)图象的公共切线,切点分别为(x1, f (x1))和(x2, g(x2)),其中x1>0.
①求证:x1>1>x2;
②若当x≥x1时,关于x的不等式ax2-x+xe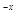 +1≤0恒成立,求实数a的取值范围.
+1≤0恒成立,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(12分)已知函数
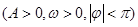 ,在同一周期内,
,在同一周期内,
当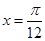 时,
时, 取得最大值
取得最大值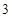 ;当
;当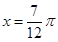 时,
时, 取得最小值
取得最小值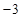 .
.
(Ⅰ)求函数 的解析式;
的解析式;
(Ⅱ)求函数 的单调递减区间;
的单调递减区间;
(Ⅲ)若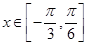 时,函数
时,函数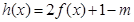 有两个零点,求实数
有两个零点,求实数 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本小题满分12分)已知函数 (
( 为常数)。
为常数)。
(Ⅰ)函数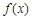 的图象在点(
的图象在点(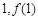 )处的切线与函数
)处的切线与函数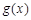 的图象相切,求实数
的图象相切,求实数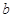 的值;
的值;
(Ⅱ)设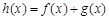 ,若函数
,若函数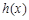 在定义域上存在单调减区间,求实数
在定义域上存在单调减区间,求实数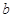 的取值范围;
的取值范围;
(Ⅲ)若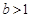 ,对于区间[1,2]内的任意两个不相等的实数
,对于区间[1,2]内的任意两个不相等的实数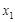 ,
,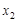 ,都有
,都有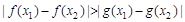 成立,求
成立,求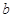 的取值范围。
的取值范围。
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
定义:若函数 对于其定义域内的某一数
对于其定义域内的某一数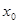 ,有
,有 ,则称
,则称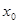 是
是 的一个不动点. 已知函数
的一个不动点. 已知函数 .
.
(1)当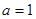 ,
,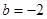 时,求函数
时,求函数 的不动点;
的不动点;
(2)若对任意的实数b,函数 恒有两个不动点,求实数
恒有两个不动点,求实数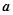 的取值范围;
的取值范围;
(3)在(2)的条件下,若 图象上两个点A、B的横坐标是函数
图象上两个点A、B的横坐标是函数 的不动点,且线段AB的中点C在函数
的不动点,且线段AB的中点C在函数 的图象上,求实数b的最小值.
的图象上,求实数b的最小值.
(参考公式:若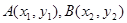 ,则线段AB的中点坐标为
,则线段AB的中点坐标为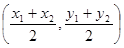 )
)
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本小题满分12分)
在经济学中,函数f(x)的边际函数Mf(x)定义为Mf(x)=f(x+1)-f(x).某公司每月生产x台某种产品的收入为R(x)元,成本为C(x)元,且R(x)=3 000x-20x2,C(x)=500x+4 000(x∈N*).现已知该公司每月生产该产品不超过100台.
(1)求利润函数P(x)以及它的边际利润函数MP(x);
(2)求利润函数的最大值与边际利润函数的最大值之差.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
武汉市某地西瓜从2012年6月1日起开始上市。通过市场调查,得到西瓜种植成本Q(单位:元/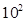 kg)与上市时间t(单位:天)的数据如下表:
kg)与上市时间t(单位:天)的数据如下表:
| 时间t | 50 | 110 | 250 |
| 种植成本Q | 150 | 108 | 150 |
 , Q= a
, Q= a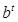 , Q=a
, Q=a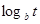 .
.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com