
(本小题满分12分)已知函数 (
( 为常数)。
为常数)。
(Ⅰ)函数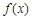 的图象在点(
的图象在点(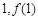 )处的切线与函数
)处的切线与函数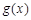 的图象相切,求实数
的图象相切,求实数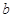 的值;
的值;
(Ⅱ)设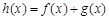 ,若函数
,若函数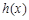 在定义域上存在单调减区间,求实数
在定义域上存在单调减区间,求实数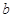 的取值范围;
的取值范围;
(Ⅲ)若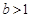 ,对于区间[1,2]内的任意两个不相等的实数
,对于区间[1,2]内的任意两个不相等的实数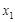 ,
,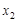 ,都有
,都有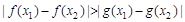 成立,求
成立,求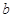 的取值范围。
的取值范围。
(Ⅰ)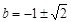 (Ⅱ)
(Ⅱ)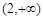 (Ⅲ)
(Ⅲ)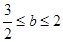
解析试题分析:(Ⅰ)因为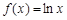 ,所以
,所以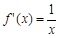 ,因此
,因此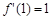 ,
,
所以函数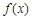 的图象在点(
的图象在点(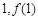 )处的切线方程为
)处的切线方程为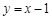 , ……1分
, ……1分
由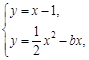 得
得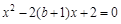 ,
,
由 ,得
,得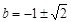 . ……3分
. ……3分
(Ⅱ)因为 ,
,
所以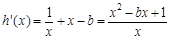 ,
,
由题意知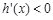 在
在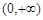 上有解,
上有解,
因为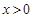 ,设
,设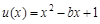 ,因为
,因为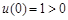 ,
,
则只要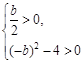 ,解得
,解得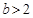 ,
,
所以b的取值范围是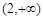 . ……6分
. ……6分
(Ⅲ)不妨设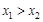 ,
,
因为函数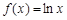 在区间[1,2]上是增函数,所以
在区间[1,2]上是增函数,所以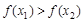 ,
,
函数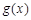 图象的对称轴为
图象的对称轴为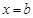 ,且
,且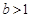 。
。
(i)当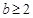 时,函数
时,函数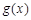 在区间[1,2]上是减函数,所以
在区间[1,2]上是减函数,所以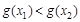 ,
,
所以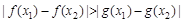 等价于
等价于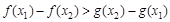 ,
,
即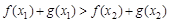 ,
,
等价于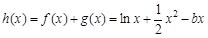 在区间[1,2]上是增函数,
在区间[1,2]上是增函数,
等价于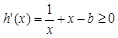 在区间[1,2]上恒成立,
在区间[1,2]上恒成立,
等价于 在区间[1,2]上恒成立,
在区间[1,2]上恒成立,
所以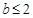 ,又
,又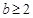 ,
,
所以 . ……8分
. ……8分
(ii)当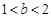 时,函数
时,函数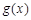 在区间[1, b]上是减函数,在
在区间[1, b]上是减函数,在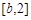 上为增函数。
上为增函数。
① 当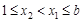 时,
时,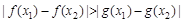 等价于
等价于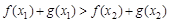 ,
,
等价于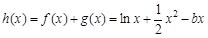 在区间[1,b]上是增函数,
在区间[1,b]上是增函数,
等价于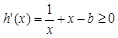 在区间[1,b]上恒成立,
在区间[1,b]上恒成立,
等价于 在区间[1,b]上恒成立,
在区间[1,b]上恒成立,
所以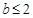 ,又
,又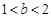 ,所以
,所以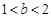
②当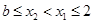 时,
时,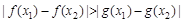 等价于
等价于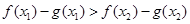 ,
,
等价于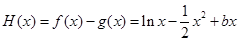 在区间[b,2]上是增函数,[来源:Z*xx*k.Com]
在区间[b,2]上是增函数,[来源:Z*xx*k.Com]
等价于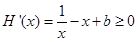 在区间[b,2]上恒成立,
在区间[b,2]上恒成立,
等价于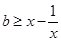 在区间[b,2]上恒成立,
在区间[b,2]上恒成立,
所以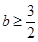 ,故
,故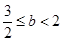 ,
,
③当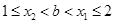 时,
时,
由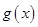 图像的对称性知,
图像的对称性知,
只要

科目:高中数学 来源: 题型:解答题
(本小题满分15分)将进货单价为80元的商品按90元一个售出时,能卖出400个,已知这种商品每个涨价1元,其销售量就减少10个,为了取得最大利润,每个售价应定为多少元?
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本小题满分12)
为了绿化城市,准备在如图所示的区域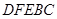 内修建一个矩形
内修建一个矩形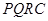 的草坪,并建立如图平面直角坐标系,且
的草坪,并建立如图平面直角坐标系,且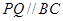 ,
,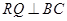 ,另外
,另外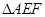 的内部有一文物保护区不能占用,经测量
的内部有一文物保护区不能占用,经测量 ,
,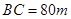 ,
, 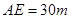 ,
,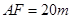 .
.
(1)求直线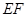 的方程;
的方程;
(2)应如何设计才能使草坪的占地面积最大?并求最大面积。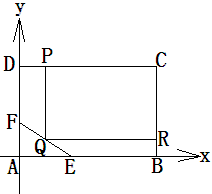
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com