
【题目】设函数f(x)=﹣ ![]() sinx
sinx ![]() cosx+1
cosx+1
(1)求函数f(x)的最小正周期和单调递增区间; (Ⅱ)若x∈[0, ![]() ],且f(x)=
],且f(x)= ![]() ,求cosx的值.
,求cosx的值.
【答案】
(1)解:(1)函数f(x)=﹣ ![]() sinx
sinx ![]() cosx+1=﹣sin(x+
cosx+1=﹣sin(x+ ![]() )+1,故该函数的最小正周期为2π,
)+1,故该函数的最小正周期为2π,
令2kπ+ ![]() ≤x+
≤x+ ![]() ≤2kπ+
≤2kπ+ ![]() ,求得2kπ+
,求得2kπ+ ![]() ≤x≤2kπ+
≤x≤2kπ+ ![]() ,可得函数的增区间为[2kπ+
,可得函数的增区间为[2kπ+ ![]() ,2kπ+
,2kπ+ ![]() ],k∈Z.
],k∈Z.
(Ⅱ)若x∈[0, ![]() ],则x+
],则x+ ![]() ∈[
∈[ ![]() ,
, ![]() ],又f(x)=
],又f(x)= ![]() ,即﹣sin(x+
,即﹣sin(x+ ![]() )+1=
)+1= ![]() ,即sin(x+
,即sin(x+ ![]() )=
)= ![]() ,
,
∴cos(x+ ![]() )=±
)=± ![]() =±
=± ![]() .
.
若cos(x+ ![]() )=﹣
)=﹣ ![]() ,则cosx=cos[(x+
,则cosx=cos[(x+ ![]() )﹣
)﹣ ![]() ]=cos(x+
]=cos(x+ ![]() ) cos
) cos ![]() +sin(x+
+sin(x+ ![]() ) sin
) sin ![]() =﹣
=﹣ ![]()
![]() +
+ ![]() =
= ![]() <0,不合题意,舍去.
<0,不合题意,舍去.
若cos(x+ ![]() )=
)= ![]() ,则cosx=cos[(x+
,则cosx=cos[(x+ ![]() )﹣
)﹣ ![]() ]=cos(x+
]=cos(x+ ![]() ) cos
) cos ![]() +sin(x+
+sin(x+ ![]() ) sin
) sin ![]() =
= ![]()
![]() +
+ ![]() =
= ![]() .
.
综上可得,cosx= ![]()
【解析】(1)利用两角和的正弦公式化简函数f(x)的解析式,再利用正弦函数的周期性和单调性,求得函数f(x)的最小正周期和单调递增区间.(Ⅱ)若x∈[0, ![]() ],利用同角三角函数的基本关系、两角差的余弦公式,求得cosx的值.
],利用同角三角函数的基本关系、两角差的余弦公式,求得cosx的值.


科目:高中数学 来源: 题型:
【题目】设函数f(x)=2x3+3ax2+3bx+8c在x=1及x=2时取得极值. (Ⅰ)求a、b的值;
(Ⅱ)若对任意的x∈[0,3],都有f(x)<c2成立,求c的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2017高考特别强调了要增加对数学文化的考查,为此某校高三年级特命制了一套与数学文化有关的专题训练卷(文、理科试卷满分均为100分),并对整个高三年级的学生进行了测试.现从这些学生中随机抽取了50名学生的成绩,按照成绩为 ![]() ,
, ![]() ,…,
,…, ![]() 分成了5组,制成了如图所示的频率分布直方图(假定每名学生的成绩均不低于50分).
分成了5组,制成了如图所示的频率分布直方图(假定每名学生的成绩均不低于50分).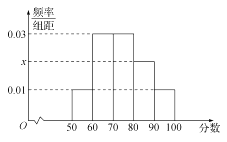
(1)求频率分布直方图中的 ![]() 的值,并估计所抽取的50名学生成绩的平均数、中位数(同一组中的数据用该组区间的中点值代表);
的值,并估计所抽取的50名学生成绩的平均数、中位数(同一组中的数据用该组区间的中点值代表);
(2)若高三年级共有2000名学生,试估计高三学生中这次测试成绩不低于70分的人数;
(3)若利用分层抽样的方法从样本中成绩不低于70分的三组学生中抽取6人,再从这6人中随机抽取3人参加这次考试的考后分析会,试求后两组中至少有1人被抽到的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设甲、乙两人每次射击命中目标的概率分别为 ![]() ,且各次射击相互独立,若按甲、乙、甲、乙…的次序轮流射击,直到有一人击中目标就停止射击,则停止射击时,甲射击了两次的概率是( )
,且各次射击相互独立,若按甲、乙、甲、乙…的次序轮流射击,直到有一人击中目标就停止射击,则停止射击时,甲射击了两次的概率是( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,角A、B、C所对应的边分别为a,b,c,若 ![]() <cosA,则△ABC为( )
<cosA,则△ABC为( )
A.锐角三角形
B.直角三角形
C.钝角三角形
D.非钝角三角形
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】函数f(x)=Asin(ωx+φ)(A>0,ω>0)的图象如图所示,为了得到g(x)=Acosωx的图象,可以将f(x)的图象( ) 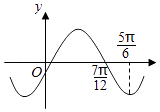
A.向左平移 ![]() 个单位长度
个单位长度
B.向左平移 ![]() 个单位长度
个单位长度
C.向右平移 ![]() 个单位长度
个单位长度
D.向右平移 ![]() 个单位长度
个单位长度
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知奇函数f(x)= 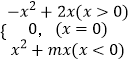 .
.
(1)求实数m的值,并在给出的直角坐标系中画出y=f(x)的图像.
(2)若函数f(x)在区间[﹣1,|a|﹣2]上单调递增,试确定a的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com