
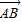 =
=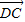 =(3,4),
=(3,4),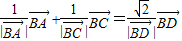 ,则四边形ABCD的面积是 .
,则四边形ABCD的面积是 . 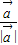 的向量,由于它的模等于1,所以它被称为单位向量.本题的向量等式的左边是两个单位向量的和,右边是和平行四边形ABCD对角线BD共线且长度等于
的向量,由于它的模等于1,所以它被称为单位向量.本题的向量等式的左边是两个单位向量的和,右边是和平行四边形ABCD对角线BD共线且长度等于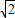 的向量,由此可以证出AB与BC互相垂直且BD平分∠ABC,从而证出四边形
的向量,由此可以证出AB与BC互相垂直且BD平分∠ABC,从而证出四边形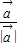 的模等于1,因而向量
的模等于1,因而向量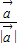 是单位向量
是单位向量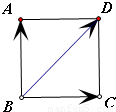
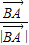 、
、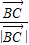 和
和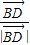 都是单位向量
都是单位向量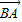 、
、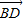 的夹角为θ,
的夹角为θ,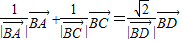
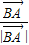 、
、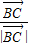 为邻边构成的四边形是菱形,可得BD在∠ABC的平分线上
为邻边构成的四边形是菱形,可得BD在∠ABC的平分线上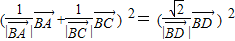 ,即1+2cosθ+1=2⇒cosθ=0⇒θ=90°
,即1+2cosθ+1=2⇒cosθ=0⇒θ=90°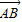 =(3,4)
=(3,4)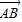 |=
|=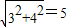


 备战中考寒假系列答案
备战中考寒假系列答案科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com