
【题目】已知五面体![]() 中,四边形
中,四边形![]() 为矩形,
为矩形,![]() ,
,![]() ,且二面角
,且二面角![]() 的大小为
的大小为![]() .
.
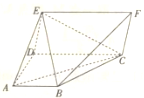
(1)证明:![]() 平面
平面![]() ;
;
(2)求二面角![]() 的余弦值.
的余弦值.
【答案】(1)见解析;(2)![]() .
.
【解析】
(1)先证![]() 平面
平面![]() ,由线面平行的性质定理得
,由线面平行的性质定理得![]() ,所以
,所以![]() 由线面垂直的判定定理得
由线面垂直的判定定理得![]() 平面
平面![]() ,从而得A
,从而得A![]() 平面
平面![]() ;
;
(2)以![]() 为坐标原点,以
为坐标原点,以![]() 所在的直线为
所在的直线为![]() 轴,过
轴,过![]() 平行于
平行于![]() 的直线为
的直线为![]() 轴,
轴,![]() 所在的直线为
所在的直线为![]() 轴,建立空间直角坐标系,
轴,建立空间直角坐标系,
(1)在五面体![]() 中,四边形
中,四边形![]() 为矩形,所以
为矩形,所以![]() ,
,![]() .
.
因为![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,所以
,所以![]() 平面
平面![]() ,
,
因为![]() 平面
平面![]() ,平面
,平面![]() 平面
平面![]() ,所以
,所以![]() ,又
,又![]() ,故
,故![]() .因为
.因为![]() ,
,![]() ,
,![]() ,所以
,所以![]() ,
,
因为![]() ,所以
,所以![]() 平面
平面![]() ,又
,又![]() ,所以
,所以![]() 平面
平面![]() .
.
(2)过点![]() 作
作![]() ,垂足为
,垂足为![]() ,以
,以![]() 为坐标原点,以
为坐标原点,以![]() 所在的直线为
所在的直线为![]() 轴,过
轴,过![]() 平行于
平行于![]() 的直线为
的直线为![]() 轴,
轴,![]() 所在的直线为
所在的直线为![]() 轴,建立如图所示的空间直角坐标系,分别求平面
轴,建立如图所示的空间直角坐标系,分别求平面![]() ,平面
,平面![]() 的法向量,利用向量法求解即可.
的法向量,利用向量法求解即可.

则![]() ,
,![]() ,
,![]() ,
,![]() ,
,
![]() ,
,![]() ,
,![]() ,
,
设平面![]() 的一个法向量为
的一个法向量为![]() ,则
,则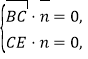 即
即
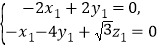 ,
,
不妨令![]() ,则
,则![]() .
.
设平面![]() 的一个法向量为
的一个法向量为![]() ,则
,则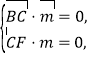 即
即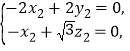
不妨令![]() ,则
,则![]() ,则
,则![]() .
.
由图知二面角![]() 为锐角,所以二面角
为锐角,所以二面角![]() 的余弦值为
的余弦值为![]() .
.


 习题精选系列答案
习题精选系列答案科目:高中数学 来源: 题型:
【题目】在![]() 中,已知
中,已知![]() 、
、![]() .
.
(1)若点![]() 的坐标为
的坐标为![]() ,直线
,直线![]() ,直线
,直线![]() 交
交![]() 边于
边于![]() ,交
,交![]() 边于
边于![]() ,且
,且![]() 与
与![]() 的面积之比为
的面积之比为![]() ,求直线
,求直线![]() 的方程;
的方程;
(2)若![]() 是一个动点,且
是一个动点,且![]() 的面积为
的面积为![]() ,试求
,试求![]() 关于
关于![]() 的函数关系式.
的函数关系式.
查看答案和解析>>
科目:高中数学 来源: 题型:
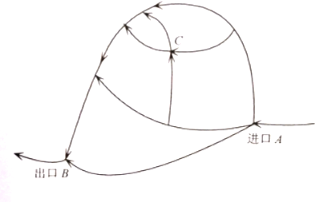
【题目】如图是一旅游景区供游客行走的路线图,假设从进口![]() 开始到出口
开始到出口![]() ,每遇到一个岔路口,每位游客选择其中一条道路行进是等可能的.现有甲、乙、丙、丁共
,每遇到一个岔路口,每位游客选择其中一条道路行进是等可能的.现有甲、乙、丙、丁共![]() 名游客结伴到旅游景区游玩,他们从进口
名游客结伴到旅游景区游玩,他们从进口![]() 的岔路口就开始选择道路自行游玩,并按箭头所指路线行走,最后到出口
的岔路口就开始选择道路自行游玩,并按箭头所指路线行走,最后到出口![]() 集中,设点
集中,设点![]() 是其中的一个交叉路口点.
是其中的一个交叉路口点.
(1)求甲经过点![]() 的概率;
的概率;
(2)设这![]() 名游客中恰有
名游客中恰有![]() 名游客都是经过点
名游客都是经过点![]() ,求随机变量
,求随机变量![]() 的概率分布和数学期望.
的概率分布和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一次足球邀请赛共安排了![]() 支球队参加,每支球队预定的比赛场数分别是
支球队参加,每支球队预定的比赛场数分别是![]() ,
,![]() ,…,
,…,![]() .若任两支球队之间至多安排了一场比赛,则称
.若任两支球队之间至多安排了一场比赛,则称![]() 是一个“有效安排”.证明:若
是一个“有效安排”.证明:若![]() 是一个有效安排,且
是一个有效安排,且![]() ,则可去掉一支球队,并重新调整各队之间的对局情况,使
,则可去掉一支球队,并重新调整各队之间的对局情况,使![]() 也是一个有效安排.
也是一个有效安排.
查看答案和解析>>
科目:高中数学 来源: 题型:
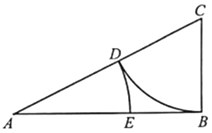
【题目】古希腊雅典学派算学家欧道克萨斯提出了“黄金分割”的理论,利用尺规作图可画出己知线段的黄金分割点,具体方法如下:(l)取线段AB=2,过点B作AB的垂线,并用圆规在垂线上截取BC=![]() AB,连接AC;(2)以C为圆心,BC为半径画弧,交AC于点D;(3)以A为圆心,以AD为半径画弧,交AB于点E.则点E即为线段AB的黄金分割点.若在线段AB上随机取一点F,则使得BE≤AF≤AE的概率约为( )(参考数据:
AB,连接AC;(2)以C为圆心,BC为半径画弧,交AC于点D;(3)以A为圆心,以AD为半径画弧,交AB于点E.则点E即为线段AB的黄金分割点.若在线段AB上随机取一点F,则使得BE≤AF≤AE的概率约为( )(参考数据:![]() 2.236)
2.236)
A. 0.236B. 0.382C. 0.472D. 0.618
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】出租车几何学是由十九世纪的赫尔曼·闵可夫斯基所创立的.在出租车几何学中,点还是形如![]() 的有序实数对,直线还是满足
的有序实数对,直线还是满足![]() 的所有
的所有![]() 组成的图形,角度大小的定义也和原来一样.直角坐标系内任意两点
组成的图形,角度大小的定义也和原来一样.直角坐标系内任意两点![]() ,
,![]() ,定义它们之间的一种“距离”:
,定义它们之间的一种“距离”:![]() ;到两点P.Q“距离”相等的点的轨迹称为线段PQ的“垂直平分线”.已知点
;到两点P.Q“距离”相等的点的轨迹称为线段PQ的“垂直平分线”.已知点![]() 、
、![]() 、
、![]() ,请解决以下问题:
,请解决以下问题:
(1)求线段![]()
![]() 上一点
上一点![]() 到原点
到原点![]() 的“距离”;
的“距离”;
(2)写出线段AB的“垂直平分线”的轨迹方程,并作出大致图像;
(3)定义:若三角形三边的“垂直平分线”交于一点,则该点称为三角形的“外心”.试判断![]() 的“外心”是否存在,如果存在,求出“外心”;如果不存在,说明理由.
的“外心”是否存在,如果存在,求出“外心”;如果不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】椭圆![]() 的离心率是
的离心率是![]() ,过点
,过点![]() 的动直线
的动直线![]() 与椭圆相交于
与椭圆相交于![]() 两点,当直线
两点,当直线![]() 与
与![]() 轴平行时,直线
轴平行时,直线![]() 被椭圆
被椭圆![]() 截得的线段长为
截得的线段长为![]() .
.
(Ⅰ)求椭圆![]() 的方程;
的方程;
(Ⅱ)在![]() 轴上是否存在异于点
轴上是否存在异于点![]() 的定点
的定点![]() ,使得直线
,使得直线![]() 变化时,总有
变化时,总有![]() ?若存在,求出点
?若存在,求出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知动圆P恒过定点![]() ,且与直线
,且与直线![]() 相切.
相切.
(Ⅰ)求动圆P圆心的轨迹M的方程;
(Ⅱ)正方形ABCD中,一条边AB在直线y=x+4上,另外两点C、D在轨迹M上,求正方形的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com