练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】设、是两条不同的直线， ， ， 是三个不同的平面，给出下列四个命题：

    ①若， ，则 ②若， ， ，则

    ③若， ，则 ④若， ，则

    其中正确命题的序号是（ ）．

    A. ①和② B. ②和③ C. ③和④ D. ①和④

    【答案】A

    【解析】对于①，因为，所以经过作平面，使，可得，

    又因为， ，所以，结合得．由此可得①是真命题；

    对于②，因为且，所以，

    结合，可得，故②是真命题；

    对于③，设直线、是位于正方体上底面所在平面内的相交直线，

    而平面是正方体下底面所在的平面，

    则有且成立，但不能推出，故③不正确；

    对于④，设平面、、是位于正方体经过同一个顶点的三个面，

    则有且，但是，推不出，故④不正确．

    综上所述，其中正确命题的序号是①和②，

    故选： ．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】函数 ．
    （1）求函数 的最大值；
    （2）对于任意 ，且 ，是否存在实数 ，使 恒成立，若存在求出 的范围，若不存在，说明理由；
    （3）若正项数列 满足 ，且数列 的前 项和为 ，试判断 与 的大小，并加以证明．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，四棱锥 中，底面ABCD为矩形，侧面PAD为正三角形，且平面 ABCD平面， E为PD中点， AD=2.

    （Ⅰ）求证：平面 平面PCD；
    （Ⅱ）若二面角 的平面角大小 满足 ，求四棱锥 的体积.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知由实数组成的等比数列{an}的前项和为Sn ， 且满足8a4=a7 ， S7=254．
    （1）求数列{an}的通项公式；
    （2）对n∈N* ， bn= ，求数列{bn}的前n项和Tn ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知等差数列{an}的公差d≠0，它的前n项和为Sn，若S5＝70，且a2，a7，a22成等比数列．

    (1)求数列{an}的通项公式；

    (2)设数列的前n项和为Tn，求证： ≤Tn＜.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在如图所示的几何体中，面为正方形，面为等腰梯形， ， ， ， ．

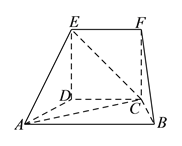
    （I）求证： 平面．

    （II）求与平面所成角的正弦值．

    （III）线段上是否存在点，使平面平面？证明你的结论．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在一次“汉马”（武汉马拉松比赛的简称）全程比赛中，50名参赛选手（24名男选手和26名女选手）的成绩（单位：分钟）分别为数据 (成绩不为0).

    （Ⅰ）24名男选手成绩的茎叶图如图⑴所示，若将男选手成绩由好到差编为1～24号，再用系统抽样方法从中抽取6人，求其中成绩在区间上的选手人数；

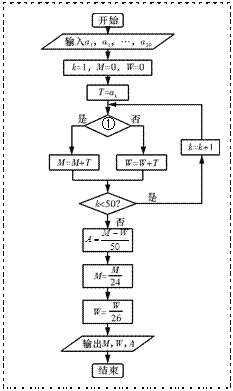
    （Ⅱ）如图⑵所示的程序用来对这50名选手的成绩进行统计.为了便于区别性别，输入时，男选手的成绩数据用正数，女选手的成绩数据用其相反数(负数)，请完成图⑵中空白的判断框①处的填写，并说明输出数值和的统计意义.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图是函数y＝f(x)的导函数y＝f′(x)的图象，则下面判断正确的是(　　 )

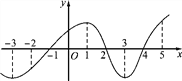
    A. 在(－2，1)上f(x)是增函数 B. 在(1，3)上f(x)是减函数

    C. 当x＝2时，f(x)取极大值 D. 当x＝4时，f(x)取极大值

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数.

    （1）求函数的最小正周期与单调递减区间；

    （2）若函数的图象上的所有点的横坐标伸长到原来的倍，所得的图象与直线交点的横坐标由小到大依次是，求的值．

    查看答案和解析>>

    同步练习册答案