
【题目】若函数![]() ,
,![]()
(1)若函数![]() 为奇函数,求m的值;
为奇函数,求m的值;
(2)若函数![]() 在
在![]() 上是增函数,求实数m的取值范围;
上是增函数,求实数m的取值范围;
(3)若函数![]() 在
在![]() 上的最小值为
上的最小值为![]() ,求实数m的值.
,求实数m的值.
【答案】(1)![]()
(2)![]()
(3)![]() 或
或![]()
【解析】
(1)由奇函数得到![]() ,代入计算得到答案.
,代入计算得到答案.
(2)讨论![]() ,
,![]() ,
,![]() 三种情况,分别计算得到答案.
三种情况,分别计算得到答案.
(3)根据(2)的讨论,分别计算函数的最小值,对比范围得到答案.
(1)![]() 是奇函数,定义域为
是奇函数,定义域为![]()
![]() ,令
,令![]() ,得
,得![]() ,
,![]()
经检验:![]() 时
时![]() ,
,![]() .
.
(2)①![]() 时,
时,![]() 开口向上,对称轴为
开口向上,对称轴为![]() ,
,
![]() 在
在![]() 上单调递增
上单调递增
②![]() 时,
时,![]() 开口向下,对称轴为
开口向下,对称轴为![]() ,
,
![]() 在
在![]() 上单调递增,在
上单调递增,在![]() 上单调递减,
上单调递减,
![]() 在
在![]() 上单调递增,
上单调递增,![]() ,
,![]() .
.
③![]() 时,
时,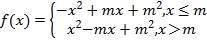
函数![]() 在
在![]() 和
和![]() 上单调递增,则
上单调递增,则![]() 上单调递减,
上单调递减,
![]() 在
在![]() 上不单调,不满足题意.
上不单调,不满足题意.
综上所述:![]() 的取值范围是
的取值范围是![]() .
.
(3)由(2)可知
①![]() 时,
时,![]() ,
,![]() 在
在![]() 上单调递增,
上单调递增,
![]() 解得
解得![]() 或
或![]()
![]()
![]()
②![]() 时,
时,![]() ,
,
![]() 在
在![]() 上单调递增,在
上单调递增,在![]() 上单调递减,
上单调递减,
当![]() 即
即![]() 时,
时,![]()
解得:![]() (舍)
(舍)
当![]() 即
即![]() 时,
时,![]()
解得:![]() ,
,![]() ,
,![]()
③![]() 时,
时,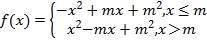
函数![]() 在
在![]() 和
和![]() 上单调递增,则
上单调递增,则![]() 上单调递减,
上单调递减,
![]() 当
当![]() 时,
时,![]()
解得:![]() (舍)
(舍)![]()
综上所述:![]() 或
或![]() .
.


 学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
学期复习一本通学习总动员期末加暑假延边人民出版社系列答案科目:高中数学 来源: 题型:
【题目】某工厂人员及工资构成如下表:
人员 | 经理 | 管理人员 | 高级技工 | 工人 | 学徒 | 合计 |
周工资/元 | 2200 | 1250 | 1220 | 1200 | 490 | |
人数 | 1 | 6 | 5 | 10 | 1 | 23 |
(1)指出这个问题中的众数、中位数、平均数.
(2)这个问题中,平均数能客观地反映该工厂的工资水平吗?为什么?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市两所高级中学联合在暑假组织全体教师外出旅游,活动分为两条线路:华东五市游和长白山之旅,且每位教师至多参加了其中的一条线路.在参加活动的教师中,高一教师占42.5%,高二教师占47.5%,高三教师占10%.参加华东五市游的教师占参加活动总人数的![]() ,且该组中,高一教师占50%,高二教师占40%,高三教师占10%.为了了解各条线路不同年级的教师对本次活动的满意程度,现用分层随机抽样的方法从参加活动的全体教师中抽取一个容量为200的样本.试确定:
,且该组中,高一教师占50%,高二教师占40%,高三教师占10%.为了了解各条线路不同年级的教师对本次活动的满意程度,现用分层随机抽样的方法从参加活动的全体教师中抽取一个容量为200的样本.试确定:
(1)参加长白山之旅的高一教师、高二教师、高三教师在该组分别所占的比例;
(2)参加长白山之旅的高一教师、高二教师、高三教师分别应抽取的人数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2018年元旦假期,高三的8名同学准备拼车去旅游,其中![]() 班、
班、![]() 班,
班,![]() 班、
班、![]() 班每班各两名,分乘甲乙两辆汽车,每车限坐4名同学
班每班各两名,分乘甲乙两辆汽车,每车限坐4名同学![]() 乘同一辆车的4名同学不考虑位置
乘同一辆车的4名同学不考虑位置![]() ,其中
,其中![]() 班两位同学是孪生姐妹,需乘同一辆车,则乘坐甲车的4名同学中恰有2名同学是来自同一个班的乘坐方式共有
班两位同学是孪生姐妹,需乘同一辆车,则乘坐甲车的4名同学中恰有2名同学是来自同一个班的乘坐方式共有![]()
![]()
A. 18种 B. 24种 C. 48种 D. 36种
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某联欢晚会举行抽奖活动,举办方设置了甲、乙两种抽奖方案,方案甲的中奖率为![]() ,中奖可以获得2分:方案乙的中奖率为
,中奖可以获得2分:方案乙的中奖率为![]() ,中奖可以获得3分;未中奖则不得分.每人有且只有一次抽奖机会,每次抽奖中奖与否互不影响,晚会结束后凭分数兑换奖品.
,中奖可以获得3分;未中奖则不得分.每人有且只有一次抽奖机会,每次抽奖中奖与否互不影响,晚会结束后凭分数兑换奖品.
(1)若小明选择方案甲抽奖,小红选择方案乙抽奖,记他们的累计得分为![]() ,求
,求![]() 的概率;
的概率;
(2)若小明、小红两人都选择方案甲或都选择方案乙进行抽奖,问:他们选择何种方案抽奖,累计得分的均值较大?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直线l:4x+3y+10=0,半径为2的圆C与l相切,圆心C在x轴上且在直线l的右上方.
(1)求圆C的方程;
(2)过点M(1,0)的直线与圆C交于A,B两点(A在x轴上方),问在x轴正半轴上是否存在定点N,使得x轴平分∠ANB?若存在,请求出点N的坐标;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com