分析:(1)由于本题中已知点A(λcosα,λsinα)(λ≠0),
B(,-),O为坐标原点,不等式
||≥2||有解即存在这样的参数使得不等式成立,这是一个存在性问题,故通过向量的模的表达公式转化为关于参数λ的不等式有解的问题,解出它的取值范围;
(2)相比(1)本小题是一个恒成立问题,可将不等式进行化简,利用三角函数的有界性转化为关于参数λ的不等式;
解答:解:(1)
||≥2||有解,即
(λcosα-)2+(λsinα+)2≥4(2分)
等价于:
λ2+1+2λsin(α-)≥4,代入
α=得:λ
2≥3(4分)
即
λ∈(-∞,-]∪[,+∞)(6分)
(2)
||≥2||对任意的实数α恒成立,即
(λcosα-)2+(λsinα+)2≥4对任意的实数α恒成立,即
λ2+1+2λsin(α-)≥4对任意的实数α恒成立 (8分)
所以
或
(12分)
解得:λ≥3或λ≤-3.故所求实数λ的取值范围是(-∞,-3]∪[3,+∞).(14分)
点评:本题是一个向量综合题,本题考查了存在性问题与恒成立问题,解此类题关键是对存在问题与恒成立问题进行转化,理解这类问题的逻辑关系是正确转化的关键,此类题是高中数学的难点,也是容易互相混淆的题,熟练掌握向量模的坐标表示公式是本题转化的知识保证,本题比较抽象,考查了推理判断能力以及计算能力,转化化归的思想,思维有深度,是高中数学中较易出错的难题



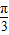 ),sin(α+
),sin(α+ )),点C(1,0).
)),点C(1,0).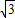 ,求α的值;
,求α的值;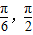 ),求
),求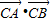 的取值范围.
的取值范围.