
【题目】已知首项均为![]() 的数列
的数列![]() ,
,![]() ,满足
,满足![]() .
.
(1)令![]() ,求数列
,求数列![]() 的通项公式;
的通项公式;
(2)若数列![]() 为各项均为正数的等比数列,且
为各项均为正数的等比数列,且![]() ,设
,设![]() ,求数列
,求数列![]() 的前
的前![]() 项和
项和![]() .
.
【答案】(1) ![]() (2)
(2) ![]()
【解析】
试题分析:(1)由题意得![]() ,从而
,从而![]() ,由此推导出数列
,由此推导出数列![]() 是首项为
是首项为![]() ,公差为
,公差为![]() 的等差数列,进而可求出数列
的等差数列,进而可求出数列![]() 的通项公式;(2)
的通项公式;(2)![]()
![]() ,
,![]() 为正项数列,∴
为正项数列,∴![]() ,∴
,∴![]() ,先分组求,利用错位相减法结合等比数列的求和公式,可求得数列
,先分组求,利用错位相减法结合等比数列的求和公式,可求得数列![]() 的前
的前![]() 项和
项和![]() .
.
试题解析:(1)![]()
![]() ,
,
即![]() ,且
,且![]() ,
,
∴![]() .
.
(2)![]()
![]() ,
,
∵![]() 为正项数列,∴
为正项数列,∴![]() ,∴
,∴![]() ,
,
∴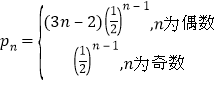 .
.
(2)方法一:
![]()
![]() ,
,
设![]()
![]()
![]()
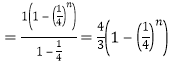 ,
,
设![]()
![]()
![]() ,
,
∴![]()
![]() ,
,
∴![]()
![]()
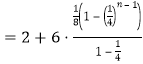
![]() ,
,
∴![]() ,
,
∴![]()
![]() .
.
方法二:
![]()
![]()
![]() ,
,
∴![]()
![]() ,
,
令![]() ,
,
∴![]()
![]() ,
,
∴![]()
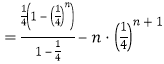
![]() ,
,
∴![]() ,
,
∴![]() .
.
【 方法点睛】本题主要考查等比数列求和公式与等差数列的通项以及错位相减法求数列的前![]() 项和,属于中档题.一般地,如果数列
项和,属于中档题.一般地,如果数列![]() 是等差数列,
是等差数列,![]() 是等比数列,求数列
是等比数列,求数列![]() 的前
的前![]() 项和时,可采用“错位相减法”求和,一般是和式两边同乘以等比数列
项和时,可采用“错位相减法”求和,一般是和式两边同乘以等比数列![]() 的公比,然后作差求解, 在写出“
的公比,然后作差求解, 在写出“![]() ”
”![]() 与“
与“![]() ” 的表达式时应特别注意将两式“错项对齐”以便下一步准确写出“
” 的表达式时应特别注意将两式“错项对齐”以便下一步准确写出“![]() ”的表达式.
”的表达式.


 全能测控期末小状元系列答案
全能测控期末小状元系列答案 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,椭圆
中,椭圆![]() 的离心率为
的离心率为![]() ,直线
,直线![]() 被椭圆
被椭圆![]() 截得的线段长为
截得的线段长为![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)过原点的直线与椭圆![]() 交于
交于![]() 两点(
两点(![]() 不是椭圆
不是椭圆![]() 的顶点),点
的顶点),点![]() 在椭圆
在椭圆![]() 上,且
上,且![]() ,直线
,直线![]() 与
与![]() 轴
轴![]() 轴分别交于
轴分别交于![]() 两点.
两点.
①设直线![]() 斜率分别为
斜率分别为![]() ,证明存在常数
,证明存在常数![]() 使得
使得![]() ,并求出
,并求出![]() 的值;
的值;
②求![]() 面积的最大值.
面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市地铁全线共有四个车站,甲、乙两人同时在地铁第1号车站(首发站)乘车,假设每人自第2号站开始,在每个车站下车是等可能的,约定用有序实数对![]() 表示“甲在
表示“甲在![]() 号车站下车,乙在
号车站下车,乙在![]() 号车站下车”
号车站下车”
(Ⅰ)用有序实数对把甲、乙两人下车的所有可能的结果列举出来;
(Ⅱ)求甲、乙两人同在第3号车站下车的概率;
(Ⅲ)求甲、乙两人在不同的车站下车的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】定义一:对于一个函数![]() ,若存在两条距离为
,若存在两条距离为![]() 的直线
的直线![]() 和
和![]() ,使得
,使得![]() 时,
时,![]() 恒成立,则称函数
恒成立,则称函数![]() 在
在![]() 内有一个宽度为
内有一个宽度为![]() 的通道.
的通道.
定义二:若一个函数![]() 对于任意给定的正数
对于任意给定的正数![]() ,都存在一个实数
,都存在一个实数![]() ,使得函数
,使得函数![]() 在
在![]() 内有一个宽度为
内有一个宽度为![]() 的通道,则称
的通道,则称![]() 在正无穷处有永恒通道.
在正无穷处有永恒通道.
下列函数①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() ;⑤
;⑤![]() . 其中在正无穷处有永恒通道的函数序号是 .
. 其中在正无穷处有永恒通道的函数序号是 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(13分)设{an}是公比为正数的等比数列a1=2,a3=a2+4.
(Ⅰ)求{an}的通项公式;
(Ⅱ)设{bn}是首项为1,公差为2的等差数列,求数列{an+bn}的前n项和Sn.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图在四棱锥![]() 中,底面
中,底面![]() 是边长为
是边长为![]() 的正方形,侧面
的正方形,侧面![]() 底面
底面![]() ,且
,且![]() ,设
,设![]() 、
、![]() 分别为
分别为![]() 、
、![]() 的中点.
的中点.
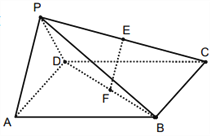
(1)求证:![]() 平面
平面![]() ;
;
(2)求证:平面![]() 平面
平面![]() ;
;
(3)求直线![]() 与平面
与平面![]() 所成角的大小.
所成角的大小.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某生物小组为了研究温度对某种酶的活性的影响进行了一组实验,得到的实验数据经整理得到如下的折线图:
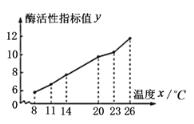
(1)由图可以看出,这种酶的活性![]() 与温度
与温度![]() 具有较强的线性相关性,请用相关系数加以说明;
具有较强的线性相关性,请用相关系数加以说明;
(2)求![]() 关于
关于![]() 的线性回归方程,并预测当温度为
的线性回归方程,并预测当温度为![]() 时,这种酶的活性指标值.(计算结果精确到0.01)
时,这种酶的活性指标值.(计算结果精确到0.01)
参考数据:![]() ,
,![]() ,
,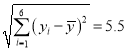 ,
,![]() .
.
参考公式:相关系数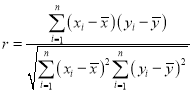 .
.
回归直线方程![]() ,
,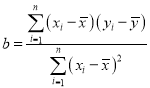 ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列命题中正确的是( )
A. 命题“![]() ”的否定是“
”的否定是“![]() ”
”
B. 命题“![]() 为真”是命题“
为真”是命题“![]() 为真”的必要不充分条件
为真”的必要不充分条件
C. 若“![]() ,则
,则![]() ”的否命题为真
”的否命题为真
D. 若实数![]() ,则满足
,则满足![]() 的概率为
的概率为![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com