
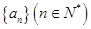 满足:
满足: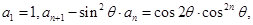 其中
其中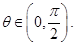
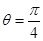 时,求
时,求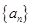 的通项公式;
的通项公式;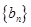 中,
中,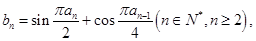 且
且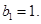 求证:对于
求证:对于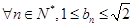 恒成立;
恒成立;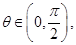 设
设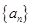 的前
的前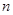 项和为
项和为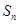 ,试比较
,试比较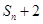 与
与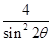 的大小.
的大小.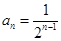 ;(2)
;(2) ;(3)
;(3)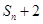 <
<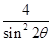 .
.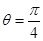 时,可求出
时,可求出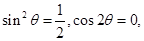 从而可得
从而可得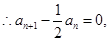 即
即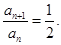 因而可确定
因而可确定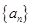 是首项为
是首项为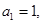 公比为
公比为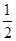 的等比数列,据此求出其通项公式;
的等比数列,据此求出其通项公式;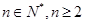 时,
时,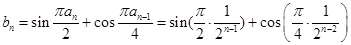 ,
,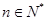 时,
时,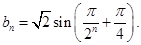
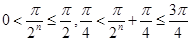 ,从得可求出
,从得可求出 .
.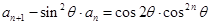 得:
得: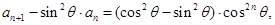
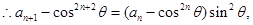
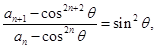
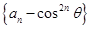 是首项为
是首项为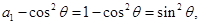 公比为
公比为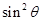 的等比数列,故
的等比数列,故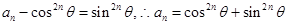 ,
,
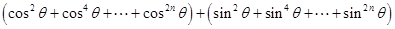 ,
,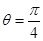 时,
时,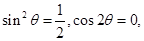
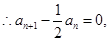 即
即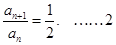 分
分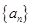 是首项为
是首项为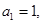 公比为
公比为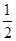 的等比数列.
的等比数列.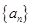 的通项公式为
的通项公式为 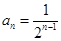 ………………………4分
………………………4分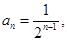
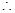 当
当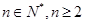 时,有
时,有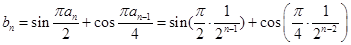
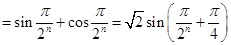 …………………6分
…………………6分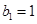 也满足上式,故当
也满足上式,故当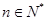 时,
时,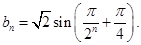
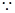
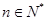 ,
,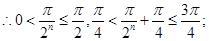
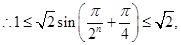 即
即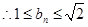 …………………………8分
…………………………8分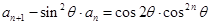 得:
得: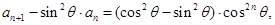
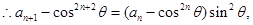
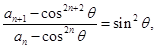
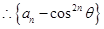 是首项为
是首项为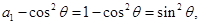 公比为
公比为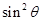 的等比数列,故
的等比数列,故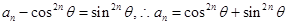 ………………9分
………………9分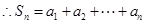
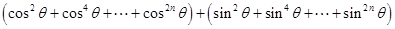
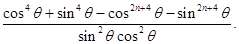 ………………………11分
………………………11分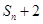 -
-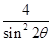 =
=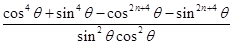
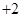 -
-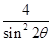
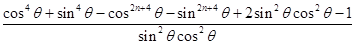
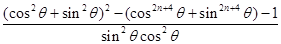
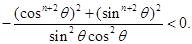
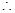
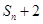 <
<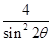 .……………………14分
.……………………14分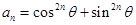 ……………………9分
……………………9分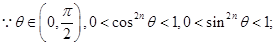 ……………………11分
……………………11分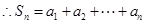
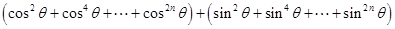

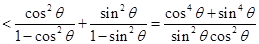
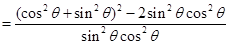
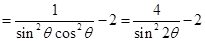
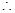
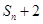 <
<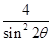 .…………………14分(其他解法酌情给分)
.…………………14分(其他解法酌情给分)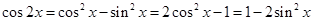 ,还有
,还有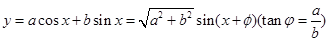 等.
等.

湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com