
所有真约数(除本身之外的正约数)的和等于它本身的正整数叫做完全数.
如: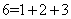 ;
;
 ;
;
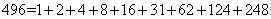 .
.
已经证明:若 是质数,则
是质数,则 是完全数,
是完全数, .请写出一个四位完全数 ;又
.请写出一个四位完全数 ;又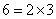 ,所以
,所以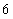 的所有正约数之和可表示为
的所有正约数之和可表示为 ;
;
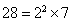 ,所以
,所以 的所有正约数之和可表示为
的所有正约数之和可表示为 ;
;
按此规律, 的所有正约数之和可表示为 .
的所有正约数之和可表示为 .
 中考利剑中考试卷汇编系列答案
中考利剑中考试卷汇编系列答案 教育世家状元卷系列答案
教育世家状元卷系列答案 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案 单元加期末复习先锋大考卷系列答案
单元加期末复习先锋大考卷系列答案科目:高中数学 来源: 题型:
 如右图述阵称为“森德拉姆筛”,记第i行第j列的数为Aij,对任意正整数为Aij,必有正整数C使得Aij+C为合数(合数的定义是:合数是除了1和它本身还能被其他的正整数整除的正整数,除2之外的偶数都是合数),则这样的C可以是( )
如右图述阵称为“森德拉姆筛”,记第i行第j列的数为Aij,对任意正整数为Aij,必有正整数C使得Aij+C为合数(合数的定义是:合数是除了1和它本身还能被其他的正整数整除的正整数,除2之外的偶数都是合数),则这样的C可以是( )查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源:学习周报 数学 北师大课标高一版(必修3) 2009-2010学年 第33期 总189期 北师大课标版 题型:044
完全数(Perfect number)是一些特殊的自然数:它所有的真因子(即除了本身以外的约数)的和,恰好等于它本身.例如:一个自然数6,它有约数1,2,3,6,除去它本身6外,其余3个数相加,即1+2+3=6,所以6是完全数.又如:8的真因子是1,2,4,而1+2+4=7,所以8不是完全数.按定义设计一个算法,判断自然数n是否为完全数.(参考式子:x Mod y表示自然数x除以y的余数,如4 Mod 3=1,8 Mod 2=0.)
查看答案和解析>>
科目:高中数学 来源: 题型:
所有真约数(除本身之外的正约数)的和等于它本身的正整数叫做完全数.
如:![]() ;
;
![]() ;
;
![]() .
.
已经证明:若![]() 是质数,则
是质数,则![]() 是完全数,
是完全数,![]() .请写出一个四位完全数 ;又
.请写出一个四位完全数 ;又![]() ,所以
,所以![]() 的所有正约数之和可表示为
的所有正约数之和可表示为![]() ;
;
![]() ,所以
,所以![]() 的所有正约数之和可表示为
的所有正约数之和可表示为![]() ;
;
按此规律,![]() 的所有正约数之和可表示为 .
的所有正约数之和可表示为 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com