
【题目】已知函数![]() .
.
(1)若函数![]() 在
在![]() 上是减函数,求实数
上是减函数,求实数![]() 的取值范围;
的取值范围;
(2)令![]() ,是否存在实数
,是否存在实数![]() ,当
,当![]() (
(![]() 是自然常数)时,函数
是自然常数)时,函数![]() 的最小值是3,若存在,求出
的最小值是3,若存在,求出![]() 的值;若不存在,说明理由.
的值;若不存在,说明理由.
(3)当![]() 时,证明:
时,证明:![]() .
.
【答案】(1)![]() ;(2)存在实数a=e2,使得当x∈(0,e]时g(x)有最小值3;(3)详见解析.
;(2)存在实数a=e2,使得当x∈(0,e]时g(x)有最小值3;(3)详见解析.
【解析】
试题分析:(1)首先将问题转化为![]() 在[1,2]上恒成立,然后将其转化为二次函数的图像及其性质即可得出所求的结果;(2)首先假设存在实数a,使g(x)=ax﹣lnx(x∈(0,e])有最小值3,并求出其导函数,然后对其进行分类讨论:①当a≤0时;②当
在[1,2]上恒成立,然后将其转化为二次函数的图像及其性质即可得出所求的结果;(2)首先假设存在实数a,使g(x)=ax﹣lnx(x∈(0,e])有最小值3,并求出其导函数,然后对其进行分类讨论:①当a≤0时;②当![]() 时;③当
时;③当![]() 时,分别利用导数研究函数的单调性并求出其最值即可得出所求的结果;(3)首先令F(x)=e2x﹣lnx,由(2)知,F(x)min,然后令
时,分别利用导数研究函数的单调性并求出其最值即可得出所求的结果;(3)首先令F(x)=e2x﹣lnx,由(2)知,F(x)min,然后令![]() ,并求出其导函数,进而得出其最大值,最后得出不等式成立.
,并求出其导函数,进而得出其最大值,最后得出不等式成立.
试题解析:(1)![]() 在[1,2]上恒成立,
在[1,2]上恒成立,
令h(x)=2x2+ax﹣1,有![]() 得
得 ,得
,得![]() .
.
(2)假设存在实数a,使g(x)=ax﹣lnx(x∈(0,e])有最小值3,![]()
①当a≤0时,g(x)在(0,e]上单调递减,g(x)min=g(e)=ae﹣1=3,![]() (舍去),
(舍去),
②当![]() 时,g(x)在
时,g(x)在![]() 上单调递减,在
上单调递减,在![]() 上单调递增
上单调递增
∴![]() ,a=e2,满足条件.
,a=e2,满足条件.
③当![]() 时,g(x)在(0,e]上单调递减,g(x)min=g(e)=ae﹣1=3,
时,g(x)在(0,e]上单调递减,g(x)min=g(e)=ae﹣1=3,![]() (舍去),
(舍去),
综上,存在实数a=e2,使得当x∈(0,e]时g(x)有最小值3.
(3)令F(x)=e2x﹣lnx,由(2)知,F(x)min=3.令![]() ,
,![]() ,
,
当0<x≤e时,'(x)≥0,φ(x)在(0,e]上单调递增∴![]()
∴![]() ,即
,即![]() .
.


科目:高中数学 来源: 题型:
【题目】某公司今年年初用25万元引进一种新的设备,投入设备后每年收益为21万元。该公司第n年需要付出设备的维修和工人工资等费用![]() 的信息如下图。
的信息如下图。
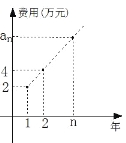
(Ⅰ)求![]() ;
;
(Ⅱ)引进这种设备后,第几年后该公司开始获利;
(Ⅲ)这种设备使用多少年,该公司的年平均获利最大?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆![]() 的方程:
的方程:![]()
(1)求m的取值范围;
(2)若圆C与直线![]() 相交于
相交于![]() ,
,![]() 两点,且
两点,且![]() ,求
,求![]() 的值
的值
(3)若(1)中的圆与直线x+2y-4=0相交于M、N两点,且OM⊥ON(O为坐标原点),求m的值;
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设椭圆![]() 的左、右焦点分别是
的左、右焦点分别是![]() ,下顶点为
,下顶点为![]() ,线段
,线段![]() 的中点为
的中点为![]() (
(![]() 为坐标原点),如图,若抛物线
为坐标原点),如图,若抛物线![]() 与
与![]() 轴的交点为
轴的交点为![]() ,且经过
,且经过![]() 点.
点.

(1)求椭圆![]() 的方程;
的方程;
(2)设![]() ,
,![]() 为抛物线
为抛物线![]() 上的一动点,过点
上的一动点,过点![]() 作抛物线
作抛物线![]() 的切线交椭圆
的切线交椭圆![]() 于点
于点![]() 、
、![]() 两点,求
两点,求![]() 面积的最大值.
面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某工厂经过市场调查,甲产品的日销售量![]() (单位:吨)与销售价格
(单位:吨)与销售价格![]() (单位:万元/吨)满足关系式
(单位:万元/吨)满足关系式 (其中
(其中![]() 为常数),已知销售价格为
为常数),已知销售价格为![]() 万元/吨时,每天可售出该产品
万元/吨时,每天可售出该产品![]() 吨.
吨.
(1)求![]() 的值;
的值;
(2)若该产品的成本价格为![]() 万元/吨,当销售价格为多少时,该产品每天的利润最大?并求出最大值.
万元/吨,当销售价格为多少时,该产品每天的利润最大?并求出最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知平面![]() 平面
平面![]() ,四边形
,四边形![]() 是正方形,四边形
是正方形,四边形![]() 是菱形,且
是菱形,且![]() ,
,![]() ,点
,点![]() 、
、![]() 分别为边
分别为边![]() 、
、![]() 的中点,点
的中点,点![]() 是线段
是线段![]() 上的动点.
上的动点.
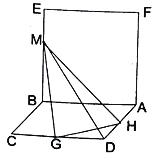
(1)求证:![]()
![]() ;
;
(2)求三棱锥![]() 的体积的最大值.
的体积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() .
.
(1)若方程![]() 有两个小于2的不等实根,求实数a的取值范围;
有两个小于2的不等实根,求实数a的取值范围;
(2)若不等式![]() 对任意
对任意![]() 恒成立,求实数a的取值范围;
恒成立,求实数a的取值范围;
(3)若函数![]() 在[0,2]上的最大值为4,求实数a的值.
在[0,2]上的最大值为4,求实数a的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com