
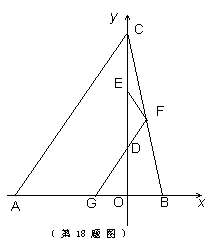
如图,![]() 的三个顶点坐标分别为
的三个顶点坐标分别为![]() ,
,![]() 分别是高
分别是高![]() 的两个三等分点,过
的两个三等分点,过![]() 作直线
作直线![]() ∥
∥![]() ,分别交
,分别交![]() 和
和![]() 于
于![]() ,连接
,连接![]() .
.
(1)求过![]() 、
、![]() 、
、![]() 三点的圆
三点的圆![]() 的方程;
的方程;
(2)在线段![]() 上是否存在点
上是否存在点![]() ,使得过点
,使得过点![]() 存在和圆M相切的直线,并且若过点
存在和圆M相切的直线,并且若过点![]() 存在两条切线时,则点
存在两条切线时,则点![]() 和两切点
和两切点![]() 组成的
组成的![]() ?若存在,求出
?若存在,求出![]() 点对应轨迹的长度;若不存在,试说明理由.
点对应轨迹的长度;若不存在,试说明理由.
 |
科目:高中数学 来源:训练必修五数学苏教版 苏教版 题型:044
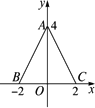
如图,△ABC三个顶点坐标为A(0,4),B(-2,0),C(2,0),求△ABC内任一点(x,y)所满足的条件.
查看答案和解析>>
科目:高中数学 来源:训练必修五数学人教A版 人教A版 题型:044
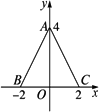
如图,△ABC三个顶点坐标为A(0,4),B(-2,0),C(2,0),求△ABC内任一点(x,y)所满足的条件.
查看答案和解析>>
科目:高中数学 来源: 题型:
(04年浙江卷理)如图,△OBC的三个顶点坐标分别为(0,0)、(1,0)、(0,2),设P1为线段BC的中点,P2为线段CO的中点,P3为线段OP1的中点,对于每一个正整数n,Pn+3为线段PnPn+1的中点,令Pn的坐标为(xn,yn),an=![]() yn+yn+1+yn+2.
yn+yn+1+yn+2.
(1)求a1,a2,a3及an;
(2)证明![]() ,nÎN*;
,nÎN*;
(3)若记bn=y4n+4-y4n,nÎN*,证明{bn}是等比数列。

查看答案和解析>>
科目:高中数学 来源: 题型:

如图,△OBC的三个顶点坐标分别为(0,0)、(1,0)、(0,2),设P1为线段BC的中点,P2为线段CO的中点,P3为线段OP1的中点,对于每一个正整数n,Pn+3为线段PnPn+1的中点,令Pn的坐标为(xn,yn),an=![]() yn+yn+1+yn+2.
yn+yn+1+yn+2.
(Ⅰ)求a1,a2,a3及an;
(Ⅱ)证明:yn+4=1-![]() ,n∈N*;
,n∈N*;
(Ⅲ)若记bn=y4n+4-y4n,n∈N*,证明:{bn}是等比数列.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com