
【题目】
如图,平行四边形![]() 中,
中,![]() ,
,![]() 将
将![]() 沿
沿![]() 折起到
折起到![]() 的位置,使平面
的位置,使平面![]() 平面
平面![]() .
.
(Ⅰ)求证:![]() ;
;
(Ⅱ)求三棱锥![]() 的侧面积.
的侧面积.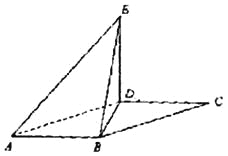
【答案】(Ⅰ)证明见解析.
(Ⅱ)![]()
【解析】
试题(1)在△ABD 中,∵AB=2,AD=4,∠DAB=60°,
∴BD=![]() .
.
∴AB2+BD2=AD2,∴AB⊥BD.
又∵平面EBD⊥平面ABD,
平面EBD∩平面ABD=BD,AB![]() 平面ABD,
平面ABD,
∴AB⊥平面EBD. 又∵DE![]() 平面EBC,∴AB⊥DE. ……5分
平面EBC,∴AB⊥DE. ……5分
(2)由(1)知AB⊥BD.
∵CD∥AB ∴CD⊥BD,从而DE⊥BD
在Rt△DBE中, ∵DB=2![]() ,DE=DC=AB=2,
,DE=DC=AB=2,
∴S△DBE=![]() .……7分
.……7分
又∵AB⊥平面EBD,BE![]() 平面EBD,∴AB⊥BE.
平面EBD,∴AB⊥BE.
∵BE=BC=AD=4,S△ABE=![]() AB·BE=4……9分
AB·BE=4……9分
∵DE⊥BD,平面EBD⊥平面ABD,∴ED⊥平面ABD,
而AD![]() 平面ABD,∴ED⊥AD,∴S△ADE=
平面ABD,∴ED⊥AD,∴S△ADE=![]() AD·DE="4." ……11分
AD·DE="4." ……11分
综上,三棱锥E—ABD的侧面积S=8+2![]() . ……12分
. ……12分


科目:高中数学 来源: 题型:
【题目】如图,CM,CN为某公园景观湖胖的两条木栈道,∠MCN=120°,现拟在两条木栈道的A,B处设置观景台,记BC=a,AC=b,AB=c(单位:百米)
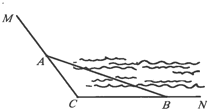
(1)若a,b,c成等差数列,且公差为4,求b的值;
(2)已知AB=12,记∠ABC=θ,试用θ表示观景路线A-C-B的长,并求观景路线A-C-B长的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】华为手机作为华为公司三大核心业务之一,2018年的销售量跃居全球第二名.某机构随机选取了100名华为手机的顾客进行调查,并将这100人的手机价格按照![]() ,
,![]() ,…,
,…,![]() 分成7组,制成如图所示的频率分布直方图.
分成7组,制成如图所示的频率分布直方图.
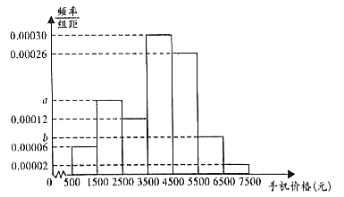
(1)若![]() 是
是![]() 的2倍,求
的2倍,求![]() ,
,![]() 的值;
的值;
(2)求这100名顾客手机价格的平均数和中位数(同一组中的数据用该组区间的中间值作代表,精确到个位);
(3)利用分层抽样的方式从手机价格在![]() 和
和![]() 的顾客中选取6人,并从这6人中随机抽取2人进行回访,求抽取的2人手机价格在不同区间的概率.
的顾客中选取6人,并从这6人中随机抽取2人进行回访,求抽取的2人手机价格在不同区间的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校高一、高二年级的全体学生都参加了体质健康测试,测试成绩满分为100分,规定测试成绩在![]() 之间为“体质优秀”,在
之间为“体质优秀”,在![]() 之间为“体质良好”,在
之间为“体质良好”,在![]() 之间为“体质合格”,在
之间为“体质合格”,在![]() 之间为“体质不合格”.现从这两个年级中各随机抽取7名学生,测试成绩如下:
之间为“体质不合格”.现从这两个年级中各随机抽取7名学生,测试成绩如下:

其中m,n是正整数.
(Ⅰ)若该校高一年级有280学生,试估计高一年级“体质优秀”的学生人数;
(Ⅱ)若从高一年级抽取的7名学生中随机抽取2人,记X为抽取的2人中为“体质良好”的学生人数,求X的分布列及数学期望;
(Ⅲ)设两个年级被抽取学生的测试成绩的平均数相等,当高二年级被抽取学生的测试成绩的方差最小时,写出m,n的值.(只需写出结论)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() ,且
,且![]() 在区间
在区间![]() 上是增函数.
上是增函数.
(1)求实数![]() 的值组成的集合
的值组成的集合![]() ;
;
(2)设函数![]() 的两个极值点为
的两个极值点为![]() 、
、![]() ,试问:是否存在实数
,试问:是否存在实数![]() ,使得不等式
,使得不等式![]() 对任意
对任意![]() 及
及![]() 恒成立?若存在,求
恒成立?若存在,求![]() 的取值范围;若不存在,请说明理由.
的取值范围;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为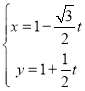 (
(![]() 为参数).以原点
为参数).以原点![]() 为极点,
为极点,![]() 轴正半轴为极轴建立极坐标系,曲线
轴正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程
的极坐标方程![]() .
.
(Ⅰ)求直线![]() 的极坐标方程和曲线
的极坐标方程和曲线![]() 的直角坐标方程;
的直角坐标方程;
(Ⅱ)若直线![]() 与曲线
与曲线![]() 交于
交于![]() ,
,![]() 两点,求
两点,求![]() 的大小.
的大小.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知曲线![]() 的参数方程为:
的参数方程为:![]() (
(![]() 为参数),
为参数),![]() 的参数方程为:
的参数方程为:![]() (
(![]() 为参数).
为参数).
(1)化![]() 、
、![]() 的参数方程为普通方程,并说明它们分别表示什么曲线;
的参数方程为普通方程,并说明它们分别表示什么曲线;
(2)若直线![]() 的极坐标方程为:
的极坐标方程为:![]() ,曲线
,曲线![]() 上的点
上的点![]() 对应的参数
对应的参数![]() ,曲线
,曲线![]() 上的点
上的点![]() 对应的参数
对应的参数![]() ,求
,求![]() 的中点
的中点![]() 到直线
到直线![]() 的距离.
的距离.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() .
.
(1)若函数![]() 在
在![]() 上单调递增,求实数
上单调递增,求实数![]() 的取值范围;
的取值范围;
(2)若函数![]() 有两个不同的零点
有两个不同的零点![]() .
.
(ⅰ)求实数![]() 的取值范围;
的取值范围;
(ⅱ)求证:![]() .(其中
.(其中![]() 为
为![]() 的极小值点)
的极小值点)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com