
【题目】在平行六面体![]() 中,
中,![]() .
.
求证:(1)![]() ;
;
(2)![]() .
.
【答案】答案见解析
【解析】分析:(1)先根据平行六面体得线线平行,再根据线面平行判定定理得结论;(2)先根据条件得菱形ABB1A1,再根据菱形对角线相互垂直,以及已知垂直条件,利用线面垂直判定定理得线面垂直,最后根据面面垂直判定定理得结论.
详解:
证明:(1)在平行六面体ABCD-A1B1C1D1中,AB∥A1B1.
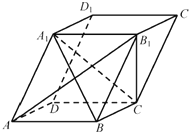
因为AB![]() 平面A1B1C,A1B1
平面A1B1C,A1B1![]() 平面A1B1C,
平面A1B1C,
所以AB∥平面A1B1C.
(2)在平行六面体ABCD-A1B1C1D1中,四边形ABB1A1为平行四边形.
又因为AA1=AB,所以四边形ABB1A1为菱形,
因此AB1⊥A1B.
又因为AB1⊥B1C1,BC∥B1C1,
所以AB1⊥BC.
又因为A1B∩BC=B,A1B![]() 平面A1BC,BC
平面A1BC,BC![]() 平面A1BC,
平面A1BC,
所以AB1⊥平面A1BC.
因为AB1![]() 平面ABB1A1,
平面ABB1A1,
所以平面ABB1A1⊥平面A1BC.


科目:高中数学 来源: 题型:
【题目】某地空气中出现污染,须喷洒一定量的去污剂进行处理.据测算,每喷洒1个单位的去污剂,空气中释放的浓度y(单位:毫克/立方米)随着时间x(单位:天)变化的函数关系式近似为 ,若多次喷洒,则某一时刻空气中的去污剂浓度为每次投放的去污剂在相应时刻所释放的浓度之和.由实验知,当空气中去污剂的浓度不低于4(毫克/立方米)时,它才能起到去污作用.
,若多次喷洒,则某一时刻空气中的去污剂浓度为每次投放的去污剂在相应时刻所释放的浓度之和.由实验知,当空气中去污剂的浓度不低于4(毫克/立方米)时,它才能起到去污作用.
(Ⅰ)若一次喷洒4个单位的去污剂,则去污时间可达几天?
(Ⅱ)若第一次喷洒2个单位的去污剂,6天后再喷洒![]()
![]() 个单位的去污剂,要使接下来的4天中能够持续有效去污,试求
个单位的去污剂,要使接下来的4天中能够持续有效去污,试求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,圆C的参数方程为 ![]() (θ为参数),以O为极点,x轴的非负半轴为极轴且取相同的单位长度建立极坐标系.
(θ为参数),以O为极点,x轴的非负半轴为极轴且取相同的单位长度建立极坐标系.
(1)求圆C的极坐标方程;
(2)若直线l的极坐标方程是 ![]() ,射线
,射线 ![]() 与圆C的交点为O、P,与直线l的交点为Q.求线段PQ的长.
与圆C的交点为O、P,与直线l的交点为Q.求线段PQ的长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,圆C的参数方程为 ![]() (θ为参数),以O为极点,x轴的非负半轴为极轴且取相同的单位长度建立极坐标系.
(θ为参数),以O为极点,x轴的非负半轴为极轴且取相同的单位长度建立极坐标系.
(1)求圆C的极坐标方程;
(2)若直线l的极坐标方程是 ![]() ,射线
,射线 ![]() 与圆C的交点为O、P,与直线l的交点为Q.求线段PQ的长.
与圆C的交点为O、P,与直线l的交点为Q.求线段PQ的长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某项“过关游戏”规则规定:在地![]() 关要抛掷
关要抛掷![]() 颗骰子
颗骰子![]() 次,如果这
次,如果这![]() 次抛掷所出现的点数和大于
次抛掷所出现的点数和大于![]() ,则算过关.
,则算过关.
(Ⅰ)此游戏最多能过__________关.
(Ⅱ)连续通过第![]() 关、第
关、第![]() 关的概率是__________.
关的概率是__________.
(Ⅲ)若直接挑战第![]() 关,则通关的概率是__________.
关,则通关的概率是__________.
(Ⅳ)若直接挑战第![]() 关,则通关的概率是__________.
关,则通关的概率是__________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数 ![]() (
( ![]() ),若函数F(x)=f(x)﹣3的所有零点依次记为x1 , x2 , x3 , …,xn , 且x1<x2<x3<…<xn , 则x1+2x2+2x3+…+2xn﹣1+xn= .
),若函数F(x)=f(x)﹣3的所有零点依次记为x1 , x2 , x3 , …,xn , 且x1<x2<x3<…<xn , 则x1+2x2+2x3+…+2xn﹣1+xn= .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,甲、乙两个企业的用电负荷量![]() 关于投产持续时间
关于投产持续时间![]() (单位:小时)的关系
(单位:小时)的关系![]() 均近似地满足函数
均近似地满足函数![]()
![]() .
.
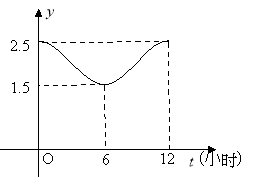
(1)根据图象,求函数![]() 的解析式;
的解析式;
(2)为使任意时刻两企业用电负荷量之和不超过![]() ,现采用错峰用电的方式,让企业乙比企业甲推迟
,现采用错峰用电的方式,让企业乙比企业甲推迟![]()
![]() 小时投产,求
小时投产,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知命题![]() 函数
函数![]() 是
是![]() 上的奇函数,命题
上的奇函数,命题![]() 函数
函数![]() 的定义域和值域都是
的定义域和值域都是![]() ,其中
,其中![]() .
.
(1)若命题![]() 为真命题,求实数
为真命题,求实数![]() 的值;
的值;
(2)若“![]() 且
且![]() ”为假命题,“
”为假命题,“![]() 或
或![]() ”为真命题,求实数
”为真命题,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com