
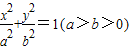 长轴的两个端点,M,N是椭圆上关于x轴对称的两点,直线AM,BN的斜率分别为k1,k2,且k1k2≠0.若|k1|+|k2|的最小值为1,则椭圆的离心率( )
长轴的两个端点,M,N是椭圆上关于x轴对称的两点,直线AM,BN的斜率分别为k1,k2,且k1k2≠0.若|k1|+|k2|的最小值为1,则椭圆的离心率( )
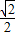
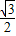
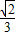
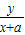 ,k2=
,k2=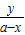
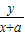 |+|
|+| |
|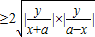 =2
=2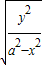 =1
=1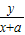 =
=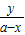 ,即x=0,y=b时等号成立
,即x=0,y=b时等号成立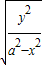 =2
=2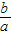 =1∴a=2b
=1∴a=2b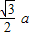
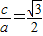


科目:高中数学 来源:2012-2013学年江西省宜春市高安中学高二(上)期末数学试卷(文科)(解析版) 题型:选择题
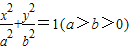 长轴的两个端点,M,N是椭圆上关于x轴对称的两点,直线AM,BN的斜率分别为k1,k2,且k1k2≠0.若|k1|+|k2|的最小值为1,则椭圆的离心率( )
长轴的两个端点,M,N是椭圆上关于x轴对称的两点,直线AM,BN的斜率分别为k1,k2,且k1k2≠0.若|k1|+|k2|的最小值为1,则椭圆的离心率( )
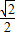
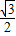
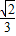
查看答案和解析>>
科目:高中数学 来源:2012-2013学年辽宁省沈阳二中等重点中学协作体高考预测数学试卷09(理科)(解析版) 题型:选择题
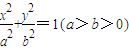 长轴的两个端点,M,N是椭圆上关于x轴对称的两点,直线AM,BN的斜率分别为k1,k2,且k1k2≠0.若|k1|+|k2|的最小值为1,则椭圆的离心率( )
长轴的两个端点,M,N是椭圆上关于x轴对称的两点,直线AM,BN的斜率分别为k1,k2,且k1k2≠0.若|k1|+|k2|的最小值为1,则椭圆的离心率( )
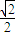
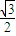
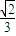
查看答案和解析>>
科目:高中数学 来源:2010年浙江省绍兴市高考数学一模试卷(理科)(解析版) 题型:选择题
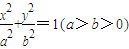 长轴的两个端点,M,N是椭圆上关于x轴对称的两点,直线AM,BN的斜率分别为k1,k2,且k1k2≠0.若|k1|+|k2|的最小值为1,则椭圆的离心率( )
长轴的两个端点,M,N是椭圆上关于x轴对称的两点,直线AM,BN的斜率分别为k1,k2,且k1k2≠0.若|k1|+|k2|的最小值为1,则椭圆的离心率( )
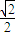
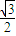
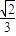
查看答案和解析>>
科目:高中数学 来源:2010年浙江省绍兴市高考数学一模试卷(文科)(解析版) 题型:选择题
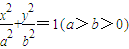 长轴的两个端点,M,N是椭圆上关于x轴对称的两点,直线AM,BN的斜率分别为k1,k2,且k1k2≠0.若|k1|+|k2|的最小值为1,则椭圆的离心率( )
长轴的两个端点,M,N是椭圆上关于x轴对称的两点,直线AM,BN的斜率分别为k1,k2,且k1k2≠0.若|k1|+|k2|的最小值为1,则椭圆的离心率( )

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com