
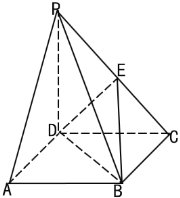
【题目】如图,四棱锥![]() 中,
中,![]() 平面
平面![]() ,底面
,底面![]() 是正方形,且
是正方形,且![]() ,
,![]() 为
为![]() 中点.
中点.
![]()
(1)求证:![]() 平面
平面![]() ;
;
(2)求二面角![]() 的余弦值.
的余弦值.
【答案】(1)证明见解析(2)![]()
【解析】
(1)由![]() 平面
平面![]() ,可得
,可得![]() ,再由正方形
,再由正方形![]() 中,得
中,得![]() ,由线面垂直的判定定理可得
,由线面垂直的判定定理可得![]() 平面
平面![]() ,从而可得
,从而可得![]() ,再由等腰三角形的性质可得
,再由等腰三角形的性质可得![]() ,可得证;
,可得证;
(2)以点![]() 为坐标原点,分别以直线
为坐标原点,分别以直线![]() 为
为![]() 轴,
轴,![]() 轴,
轴,![]() 轴,建立空间直角坐标系,再分别求出面
轴,建立空间直角坐标系,再分别求出面![]() 的一个法向量和平面
的一个法向量和平面![]() 的一个法向量,再由向量的夹角运算可求得二面角的余弦值.
的一个法向量,再由向量的夹角运算可求得二面角的余弦值.
解:(1)证明:![]() 平面
平面![]() ,
,![]() ,
,
又正方形![]() 中,
中,![]() ,
,![]() 平面
平面![]() ,
,
又![]() 平面
平面![]() ,
,![]() ,
,![]() ,
,![]() 是
是![]() 的中点,
的中点,
所以![]() ,
,![]() 平面
平面![]()
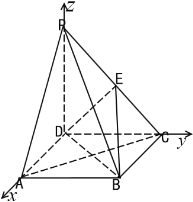
(2)以点![]() 为坐标原点,分别以直线
为坐标原点,分别以直线![]() 为
为![]() 轴,
轴,![]() 轴,
轴,![]() 轴,建立如下图所示的空间直角坐标系,由题意知:
轴,建立如下图所示的空间直角坐标系,由题意知:
![]() ,
,![]()
设平面![]() 的法向量为
的法向量为![]() ,则
,则![]() ,
,
![]() ,令
,令![]() ,得到
,得到![]() ,
,![]() ,
,
![]() 平面
平面![]() ,
,![]() ,
,
又正方形![]() 中,
中,![]() ,
,![]() 平面
平面![]()
又![]() ,
,
![]() 平面
平面![]() 的一个法向量为
的一个法向量为![]() ,
,
设二面角![]() 的平面角为
的平面角为![]() ,由图示可知二面角
,由图示可知二面角![]() 为锐角,
为锐角,
则![]() .
.![]() 二面角
二面角![]() 的余弦值为
的余弦值为![]() .
.


科目:高中数学 来源: 题型:
【题目】若数列![]() 、
、![]() 满足
满足![]() (
(![]() N*),则称
N*),则称![]() 为数列
为数列![]() 的“偏差数列”.
的“偏差数列”.
(1)若![]() 为常数列,且为
为常数列,且为![]() 的“偏差数列”,试判断
的“偏差数列”,试判断![]() 是否一定为等差数列,并说明理由;
是否一定为等差数列,并说明理由;
(2)若无穷数列![]() 是各项均为正整数的等比数列,且
是各项均为正整数的等比数列,且![]() ,
,![]() 为数列
为数列![]() 的“偏差数列”,求
的“偏差数列”,求![]() 的值;
的值;
(3)设![]() ,
,![]() 为数列
为数列![]() 的“偏差数列”,
的“偏差数列”,![]() ,
,![]() 且
且![]() ,若
,若![]() 对任意
对任意![]() 恒成立,求实数M的最小值.
恒成立,求实数M的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设椭圆![]()
![]() 的左、右焦点分别为
的左、右焦点分别为![]() ,过
,过![]() 的直线交椭圆于
的直线交椭圆于![]() 两点,若椭圆C的离心率为
两点,若椭圆C的离心率为![]() ,
,![]() 的周长为8.
的周长为8.
(Ⅰ)求椭圆C的方程;
(Ⅱ)已知直线![]() 与椭圆C交于
与椭圆C交于![]() 两点,是否存在实数k使得以
两点,是否存在实数k使得以![]() 为直径的圆恰好经过坐标原点?若存在,求出k的值;若不存在,请说明理由.
为直径的圆恰好经过坐标原点?若存在,求出k的值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某地因受天气,春季禁渔等因素影响,政府规定每年的7月1日以后的100天为当年的捕鱼期.某渔业捕捞队对吨位为![]() 的20艘捕鱼船一天的捕鱼量进行了统计,如下表所示:
的20艘捕鱼船一天的捕鱼量进行了统计,如下表所示:
捕鱼量(单位:吨) |
|
|
|
|
|
频数 | 2 | 7 | 7 | 3 | 1 |
根据气象局统计近20年此地每年100天的捕鱼期内的晴好天气情况如下表(捕鱼期内的每个晴好天气渔船方可捕鱼,非晴好天气不捕鱼):
晴好天气(单位:天) |
|
|
|
|
|
频数 | 2 | 7 | 6 | 3 | 2 |
(同组数据以这组数据的中间值作代表)
(Ⅰ)估计渔业捕捞队吨位为![]() 的渔船一天的捕鱼量的平均数;
的渔船一天的捕鱼量的平均数;
(Ⅱ)若以(Ⅰ)中确定的平均数作为上述吨位的捕鱼船在晴好天气捕鱼时一天的捕鱼量.
①估计一艘上述吨位的捕鱼船一年在捕鱼期内的捕鱼总量;
②已知当地鱼价为2万元/吨,此种捕鱼船在捕鱼期内捕鱼时,每天成本为10万元/艘;若不捕鱼,每天成本为2万元/艘,请依据往年天气统计数据,估计一艘此种捕鱼船年利润不少于1600万元的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
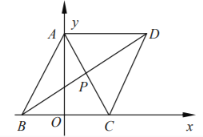
【题目】如图,在平行四边形![]() 中,点
中,点![]() ,
,![]() ,
,![]() ,对角线
,对角线![]() ,
,![]() 交于点P.
交于点P.
(1)求直线![]() 的方程;
的方程;
(2)若点E,F分别在平行四边形![]() 的边
的边![]() 和
和![]() 上运动,且
上运动,且![]() ,求
,求![]() 的取值范围;
的取值范围;
(3)试写出三角形![]() 区域(包括边界)所满足的线性约束条件,若在该区域上任取一点M,使
区域(包括边界)所满足的线性约束条件,若在该区域上任取一点M,使![]() ,试求
,试求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某年数学竞赛邀请了一位来自![]() 星球的选手参加填空题比赛,共10道题目,这位选手做题有一个古怪的习惯:先从最后一题(第10题)开始往前看,凡是遇到会的题目就作答,遇到不会的题目先跳过(允许跳过所有的题目),一直看到第1题,然后从第1题开始往后看,凡是遇到先前未答的题目就随便写个答案,遇到先前已答得题目则跳过(例如,他可以按照9、8、7、4、3、2、1、5、6、10的次序答题),这样所有题目均有作答,则这位选手可能的答题次序有______种.
星球的选手参加填空题比赛,共10道题目,这位选手做题有一个古怪的习惯:先从最后一题(第10题)开始往前看,凡是遇到会的题目就作答,遇到不会的题目先跳过(允许跳过所有的题目),一直看到第1题,然后从第1题开始往后看,凡是遇到先前未答的题目就随便写个答案,遇到先前已答得题目则跳过(例如,他可以按照9、8、7、4、3、2、1、5、6、10的次序答题),这样所有题目均有作答,则这位选手可能的答题次序有______种.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com