
(1)求数列{an}的通项公式;
(2)求证:f(![]() )<1.
)<1.
思路解析:从f(1)=n2知,数列{an}的前n项和Sn=n2,这样,就将问题转化为“知Sn求an”的问题了.
解:(1)在f(x)中,令x=1,则f(1)=a1+a2+a3+…+an,
∵ f(1)=n2,∴ a1+a2+a3+…+an=n2,即Sn=n2.
当n=1时,a1=S1=1,
当n≥2时,an=Sn-Sn-1=n2-(n-1)2=2n-1.
验证知,a1=1也适合上式,∴ an=2n-1(n∈N*).
(2)∵ f(![]() )=
)=![]() +3×(
+3×(![]() )2+5×(
)2+5×(![]() )3+…+(2n-1)×(
)3+…+(2n-1)×(![]() )n,
)n,
∴ ![]() f(
f(![]() )=1×(
)=1×(![]() )2+3×(
)2+3×(![]() )3+…+(2n-3)×(
)3+…+(2n-3)×(![]() )n+(2n-1)×(
)n+(2n-1)×(![]() )n+1.
)n+1.
两式相减,得![]() f(
f(![]() )=
)=![]() +2[(
+2[(![]() )2+(
)2+(![]() )3+…+(
)3+…+(![]() )n]-(2n-1)×(
)n]-(2n-1)×(![]() )n+1
)n+1
=![]() +2×
+2×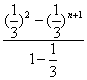 -(2n-1)×(
-(2n-1)×(![]() )n+1=
)n+1=![]() -2(n+1)(
-2(n+1)(![]() )n+1,
)n+1,
∴ f(![]() )=1-(n+1)(
)=1-(n+1)(![]() )n<1.
)n<1.
评注:此题综合了数列与函数,数列与不等式,及数列求和等多方面的知识,值得研究.


科目:高中数学 来源: 题型:
| a-x2 |
| x |
| 1 |
| 2 |
| 1 |
| 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
|
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com