
| 3 |
科目:高中数学 来源: 题型:
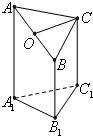 如图是一个直三棱柱(以A1B1C1为底面)被一平面所截得到的几何体,截面为ABC.已知A1B1=B1C1=1,∠A1B1C1=90°,AA1=4,BB1=2,CC1=3.
如图是一个直三棱柱(以A1B1C1为底面)被一平面所截得到的几何体,截面为ABC.已知A1B1=B1C1=1,∠A1B1C1=90°,AA1=4,BB1=2,CC1=3.查看答案和解析>>
科目:高中数学 来源: 题型:044
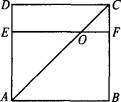
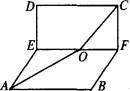
如图,ABCD是正方形,E、F分别是AD、Bc边上的点,EF∥AB,EF交AC于点O,以EF为棱把它折成直二面角A—EF—D后,求证:不论EF怎样移动,∠AOC是定值.
查看答案和解析>>
科目:高中数学 来源:数学教研室 题型:044
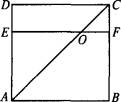
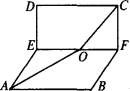
查看答案和解析>>
科目:高中数学 来源: 题型:

查看答案和解析>>
科目:高中数学 来源:陕西省宝鸡中学2010届高三适应性训练(数学理) 题型:填空题
A.(参数方程与极坐标)
直线 与直线
与直线 的夹角大小为
的夹角大小为
 B.(不等式选讲)要使关于x的不等式
B.(不等式选讲)要使关于x的不等式 在实数
在实数
范围内有解,则A的取值范围是
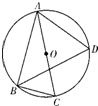
C.(几何证明选讲) 如图所示,在圆O中,AB是圆O的直
径AB =8,E为OB.的中点,CD过点E且垂直于AB,
EF⊥AC,则
CF•CA=
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com