
设α为实数,函数f(x)=x3-x2-x+a.
(Ⅰ)求f(x)的极值;
(Ⅱ)当a在什么范围内取值时,曲线y=f(x)与x轴仅有一个交点。
(21)本小题主要考查导数的概念和计算,应用导数研究函数性质的方法及推理和运算能力。
解:(Ⅰ)f’(x)=3x2-2x-1
若f’(x)=0,则x=-![]() ,1.
,1.
当x变化时,f’(x), f(x)变化情况如下表:
x | (-∞,- | - | (- | 1 | (1,+∞) |
f'(x) | + | 0 | - | 0 | + |
f(x) | ↗ | 极大值 | ↘ | 极小值 | ↗ |
所以f(x)的极大值是f(-![]() )=
)=![]() +a,极小值是f(1)=a-1.
+a,极小值是f(1)=a-1.
(Ⅱ)函数f(x)=x3-x2-x+a=(x-1)2(x+1)+a-1
由此可知x取足够大的正数时,有f(x)>0,x取足够小的负数时有f(x)<0,所以由线y=f(x)与x轴至少有一个交点。
结合f(x)的单调性可知:
当f(x)的极大值![]() +a<0,即a∈(-∞,-
+a<0,即a∈(-∞,-![]() )时,它的极小值也小于0,因此曲线y= f(x)与x轴仅有一个交点,它在(1,+∞)上;
)时,它的极小值也小于0,因此曲线y= f(x)与x轴仅有一个交点,它在(1,+∞)上;
当f(x)的极小值a-1>0,即a∈(1,+∞)时,它的极大值也大于0,因此曲线y=f(x)与x轴仅有一个交点,它在(-∞,-![]() )上。
)上。
所以当a∈(-∞,-![]() )∪(1,+∞)时,曲线y= f(x)与x轴仅有一个交点.
)∪(1,+∞)时,曲线y= f(x)与x轴仅有一个交点.


科目:高中数学 来源: 题型:
| 2 | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 2 | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 2 | 3 |
查看答案和解析>>
科目:高中数学 来源:2010-2011学年湖北省孝感市英才高中高一(下)第一次月考数学试卷(理科)(解析版) 题型:解答题
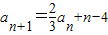 ,bn=(-1)n(an-3n+21),其中λ为实数,n为正整数.
,bn=(-1)n(an-3n+21),其中λ为实数,n为正整数.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com