
(Ⅰ)求椭圆的方程;
(Ⅱ)设P为右准线上不同于点(4,0)的任意一点,若直线AP、BP分别与椭圆相交于异于A、B的点M、N,证明点B在以MN为直径的圆内。
(此题不要求画图)
20.本小题主要考查直线、圆和椭圆等平面解析几何的基础知识,考查综合运用数学知识进行推理运算的能力和解决问题的能力。
解:(Ⅰ)依题意得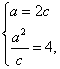 解得
解得![]() 从而b=
从而b=![]() 。
。
故椭圆方程为![]() 。
。
(Ⅱ)解法1:由(Ⅰ)得A(-2,0)B(2,0)。设M(![]()
∵M点在椭圆上,∴![]() ①
①
又M点异于项点A,B,∴ ![]()
由P、A、M三点共线可得P(4,![]() ),
),
从而![]()
∴![]() (
(![]() ). ②
). ②
将①式代入②式简化得![]()
∵2-x0>0,∴![]() >0,于是∠MBP为锐角,从而∠MBN为钝角,故点B在以MN为直径的圆内。
>0,于是∠MBP为锐角,从而∠MBN为钝角,故点B在以MN为直径的圆内。
解法2:由(Ⅰ)得A(-2,0),B(2,0),设![]() 则直线AP的方程为
则直线AP的方程为![]() 直线BP的方程为
直线BP的方程为![]()
∵点M、N分别在直线AP、BP上,
∴![]() 从而
从而![]() ③
③
联立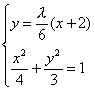 消去y得(27+
消去y得(27+![]() )
)![]()
∵![]() 是方程的两根,∴(-2)·
是方程的两根,∴(-2)·![]() ①
①
又![]()
于是由③,④式代入⑤式化简可得![]()
∵N点在椭圆上,且异于顶点A、B,∴![]()
又∵![]() ∴
∴![]() >0,从而
>0,从而![]() <0,故∠MBN为钝角,即点B在以MN为直径的圆内。
<0,故∠MBN为钝角,即点B在以MN为直径的圆内。
解法3:由(Ⅰ)得![]() 则
则![]() 又MN的中点Q的坐标为(
又MN的中点Q的坐标为(![]()


 能考试期末冲刺卷系列答案
能考试期末冲刺卷系列答案科目:高中数学 来源: 题型:
| x2 |
| a2 |
| y2 |
| b2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| x2 |
| a2 |
| y2 |
| b2 |
| ||
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| x2 |
| a2 |
| y2 |
| b2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| x2 |
| a2 |
| y2 |
| b2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| x2 |
| a2 |
| y2 |
| b2 |
| 3 |
| a2 |
| c |
| a2 |
| c |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com