
【题目】已知A、B、C为△ABC的三个内角,且其对边分别为a、b、c,若cosBcosC﹣sinBsinC= ![]() .
.
(1)求角A;
(2)若a=2 ![]() ,b+c=4,求△ABC的面积.
,b+c=4,求△ABC的面积.
【答案】
(1)解:在△ABC中,∵cosBcosC﹣sinBsinC= ![]() ,
,
∴cos(B+C)= ![]() ,
,
又∵0<B+C<π,
∴B+C= ![]() ,
,
∵A+B+C=π,
∴A= ![]()
(2)解:由余弦定理a2=b2+c2﹣2bccosA,
得(2 ![]() )2=(b+c)2﹣2bc﹣2bccos
)2=(b+c)2﹣2bc﹣2bccos ![]() ,
,
把b+c=4代入得:12=16﹣2bc+bc,
整理得:bc=4,
则△ABC的面积S= ![]() bcsinA=
bcsinA= ![]() ×4×
×4× ![]() =
= ![]()
【解析】(1)已知等式左边利用两角和与差的余弦函数公式化简,求出cos(B+C)的值,确定出B+C的度数,即可求出A的度数;(2)利用余弦定理列出关系式,再利用完全平方公式变形,将a与b+c的值代入求出bc的值,再由sinA的值,利用三角形面积公式即可求出三角形ABC面积.


科目:高中数学 来源: 题型:
【题目】某大学志愿者协会有6名男同学,4名女同学,在这10名同学中,3名同学来自数学学院,其余7名同学来自物理、化学等其他互不相同的七个学院,现从这10名同学中随机选取3名同学,到希望小学进行支教活动(每位同学被选到的可能性相同).
(1)求选出的3名同学是来自互不相同学院的概率;
(2)设X为选出的3名同学中女同学的人数,求随机变量X的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]()
(1)求函数![]() 的极值;
的极值;
(2)若![]() 时,函数
时,函数![]() 有且只有一个零点,求实数
有且只有一个零点,求实数![]() 的值;
的值;
(3若![]() ,对于区间
,对于区间![]() 上的任意两个不相等的实数
上的任意两个不相等的实数![]() ,都有
,都有![]() 成立,求实数
成立,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]()
(1)求函数![]() 的极值;
的极值;
(2)若![]() 时,函数
时,函数![]() 有且只有一个零点,求实数
有且只有一个零点,求实数![]() 的值;
的值;
(3若![]() ,对于区间
,对于区间![]() 上的任意两个不相等的实数
上的任意两个不相等的实数![]() ,都有
,都有![]() 成立,求实数
成立,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】长沙市物价监督部门为调研某公司新开发上市的一种产品销售价格的合理性,对某公司的该产品的销量与价格进行了统计分析,得到如下数据和散点图:
定价 | 10 | 20 | 30 | 40 | 50 | 60 |
年销量 | 1150 | 643 | 424 | 262 | 165 | 86 |
| 14.1 | 12.9 | 12.1 | 11.1 | 10.2 | 8.9 |

(参考数据: ![]() ,
,
![]() )
)
(1)根据散点图判断, ![]() 与
与![]() 和
和![]() 与
与![]() 哪一对具有的线性相关性较强(给出判断即可,不必说明理由)?
哪一对具有的线性相关性较强(给出判断即可,不必说明理由)?
(2)根据(1)的判断结果及数据,建立![]() 关于
关于![]() 的回归方程(方程中的系数均保留两位有效数字).
的回归方程(方程中的系数均保留两位有效数字).
(3)定价为多少元/ ![]() 时,年销售额的预报值最大?
时,年销售额的预报值最大?
附:对于一组数据![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小二乘估计分别为
的斜率和截距的最小二乘估计分别为 .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=Asin(ωx+φ)(其中A>0,ω>0,|φ|< ![]() )的部分图象如图所示.
)的部分图象如图所示. 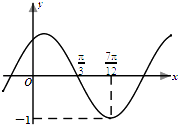
(1)求函数y=f(x)的解析式;
(2)求函数y=f(x)的单调增区间;
(3)求方程f(x)=0的解集.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知多面体![]() 的底面
的底面![]() 是边长为2的正方形,
是边长为2的正方形, ![]() 底面
底面![]() ,
, ![]() ,且
,且![]() .
.
(Ⅰ)记线段![]() 的中点为
的中点为![]() ,在平面
,在平面![]() 内过点
内过点![]() 作一条直线与平面
作一条直线与平面![]() 平行,要求保留作图痕迹,但不要求证明.
平行,要求保留作图痕迹,但不要求证明.
(Ⅱ)求直线![]() 与平面
与平面![]() 所成角的正弦值;
所成角的正弦值;

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点![]() 在圆
在圆![]() :
: ![]() 上,而
上,而![]() 为
为![]() 在
在![]() 轴上的投影,且点
轴上的投影,且点![]() 满足
满足![]() ,设动点
,设动点![]() 的轨迹为曲线
的轨迹为曲线![]() .
.
(1)求曲线![]() 的方程;
的方程;
(2)若![]() 是曲线
是曲线![]() 上两点,且
上两点,且![]() ,
, ![]() 为坐标原点,求
为坐标原点,求![]() 的面积的最大值.
的面积的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com