
【题目】设函数f(x)=|x-1|+|2x-1|.
(Ⅰ)若对 ![]() x>0,不等式f(x)≥tx恒成立,求实数t的最大值M;
x>0,不等式f(x)≥tx恒成立,求实数t的最大值M;
(Ⅱ)在(Ⅰ)成立的条件下,正实数a,b满足a2+b2=2M.证明:a+b≥2ab.
【答案】解:(Ⅰ)解: ![]() 恒成立
恒成立
![]() ∵
∵ ![]() ,
,
当且仅当 ![]() ,即
,即 ![]() 时取等号,
时取等号,
∴t≤1,∴M=1.
(Ⅱ)证明:∵a2+b2≥2ab,∴ab≤1.
∴ ![]() .(当且仅当“a=b”时取等号)①
.(当且仅当“a=b”时取等号)①
又∵ ![]() ,∴
,∴ ![]() .
.
∴ ![]() ,(当且仅当“a=b”时取等号)②
,(当且仅当“a=b”时取等号)②
由①、②得 ![]() .(当且仅当“a=b”时取等号)
.(当且仅当“a=b”时取等号)
∴a+b≥2ab
【解析】(Ⅰ)将函数不等式化为t小于等于含x代数式,即t小于等于该代数式的最小值,再利用基本不等式求得该代数式的最小值,从而求得t的最大值;(Ⅱ)根据基本不等式a2+b2≥2ab求得ab≤1,再对基本不等式变形求得结论.
【考点精析】掌握基本不等式是解答本题的根本,需要知道基本不等式:![]()
![]() ,(当且仅当
,(当且仅当![]() 时取到等号);变形公式:
时取到等号);变形公式:![]()
![]() .
.


科目:高中数学 来源: 题型:
【题目】为了调查某厂工人生产某种产品的能力,随机抽查了20位工人某天生产该产品的数量.产品数量的分组区间为[45,55),[55,65),[65,75),[75,85),[85,95)由此得到频率分布直方图如图.则产品数量位于[55,65)范围内的频率为;这20名工人中一天生产该产品数量在[55,75)的人数是 . 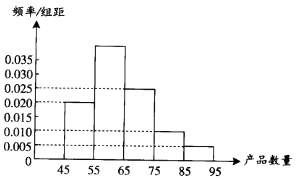
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】最新公布的《道路交通安全法》和《道路交通安全法实施条例》对车速、安全车距以及影响驾驶人反应快慢等因素均有详细规定,这些规定说到底主要与刹车距离有关,刹车距离是指从驾驶员发现障碍到制动车辆,最后完全停止所行驶的距离,即:刹车距离=反应距离+制动距离,反应距离=反应时间×速率,制动距离与速率的平方成正比,某反应时间为![]() 的驾驶员以
的驾驶员以![]() 的速率行驶,遇紧急情况,汽车的刹车距离为
的速率行驶,遇紧急情况,汽车的刹车距离为![]() .
.
(![]() )试将刹车距离
)试将刹车距离![]() 表示为速率
表示为速率![]() 的函数.
的函数.
(![]() )若该驾驶员驾驶汽车在限速为
)若该驾驶员驾驶汽车在限速为![]() 的公路上行驶,遇紧急情况,汽车的刹车距离为
的公路上行驶,遇紧急情况,汽车的刹车距离为![]() ,试问该车是否超速?请说明理由.
,试问该车是否超速?请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,等边三角形![]() 的中线
的中线![]() 与中位线
与中位线![]() 相交于
相交于![]() ,已知
,已知![]() 是
是![]() 绕
绕![]() 旋转过程中的一个图形,下列命题中,错误的是
旋转过程中的一个图形,下列命题中,错误的是

A. 恒有![]() ⊥
⊥![]()
B. 异面直线![]() 与
与![]() 不可能垂直
不可能垂直
C. 恒有平面![]() ⊥平面
⊥平面![]()
D. 动点![]() 在平面
在平面![]() 上的射影在线段
上的射影在线段![]() 上
上
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,椭圆 ![]() +
+ ![]() =1(a>b>0)的离心率为e,D为右准线上一点.
=1(a>b>0)的离心率为e,D为右准线上一点.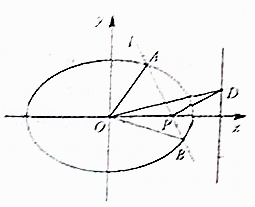
(1)若e= ![]() ,点D的横坐标为4,求椭圆的方程;
,点D的横坐标为4,求椭圆的方程;
(2)设斜率存在的直线l经过点P( ![]() ,0),且与椭圆交于A,B两点.若
,0),且与椭圆交于A,B两点.若 ![]() +
+ ![]() =
= ![]() ,DP⊥l,求椭圆离心率e.
,DP⊥l,求椭圆离心率e.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com