
【题目】在平面直角坐标系![]() 中,椭圆
中,椭圆![]() 过点
过点![]() ,焦点
,焦点![]() ,圆
,圆![]() 的直径为
的直径为![]() .
.
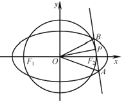
(1)求椭圆![]() 及圆
及圆![]() 的方程;
的方程;
(2)设直线![]() 与圆
与圆![]() 相切于第一象限内的点
相切于第一象限内的点![]() ,直线
,直线![]() 与椭圆
与椭圆![]() 交于
交于![]() 两点.若
两点.若![]() 的面积为
的面积为![]() ,求直线
,求直线![]() 的方程.
的方程.
【答案】(1)![]() ,
,![]() ;(2)
;(2)![]() .
.
【解析】
(1)由椭圆焦点可以确定![]() ,再利用点
,再利用点![]() 代入椭圆方程即可求出
代入椭圆方程即可求出![]() ,从而得到椭圆方程;由圆O的直径为
,从而得到椭圆方程;由圆O的直径为![]() ,即可知圆心坐标为
,即可知圆心坐标为![]() ,半径为
,半径为![]() ,从而得到圆的方程.
,从而得到圆的方程.
(2)设切点坐标为![]() ,即可表示出直线
,即可表示出直线![]() 的方程,联立直线
的方程,联立直线![]() 的方程与椭圆方程,消去
的方程与椭圆方程,消去![]() 得到关于
得到关于![]() 的一元二次方程,利用求根公式求出
的一元二次方程,利用求根公式求出![]() ,然后利用弦长公式表示
,然后利用弦长公式表示![]() ,而由条件可求出
,而由条件可求出![]() ,结合
,结合![]() ,即可求出
,即可求出![]() ,从而求出直线
,从而求出直线![]() 的方程.
的方程.
(1)因为椭圆C的焦点为![]() ,
,
可设椭圆C的方程为![]() .
.
又点![]() 在椭圆C上,所以
在椭圆C上,所以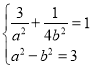 ,解得
,解得
因此,椭圆C的方程为![]() .
.
因为圆O的直径为![]() ,所以其方程为
,所以其方程为![]() .
.
(2)设直线![]() 与圆O相切于
与圆O相切于![]() ,
,
则![]() ,所以直线
,所以直线![]() 的方程为
的方程为![]() ,
,
即![]() .由
.由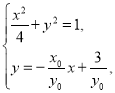 消去y,得
消去y,得
![]() ①
①
因为三角形OAB的面积为![]() ,所以
,所以![]() ,从而
,从而![]() ,
,
设![]() ,由①得
,由①得 ,
,
所以![]()
![]() .因为
.因为![]() ,
,
所以![]() ,即
,即![]() ,解得
,解得![]() 舍去),
舍去),
则![]() ,因此P的坐标为
,因此P的坐标为![]() .
.
故直线l的方程为:![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】已知三棱锥![]() (如图1)的平面展开图(如图2)中,四边形
(如图1)的平面展开图(如图2)中,四边形![]() 为边长为
为边长为![]() 的正方形,△ABE和△BCF均为正三角形,在三棱锥
的正方形,△ABE和△BCF均为正三角形,在三棱锥![]() 中:
中:
(I)证明:平面![]()
![]() 平面
平面![]() ;
;
(Ⅱ)求二面角![]() 的余弦值;
的余弦值;
(Ⅲ)若点![]() 在棱
在棱![]() 上,满足
上,满足![]() ,
, ![]() ,点
,点![]() 在棱
在棱![]() 上,且
上,且![]() ,求
,求![]() 的取值范围.
的取值范围.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直线l:kx-y+1+2k=0(k∈R).
(1)证明:直线l过定点;
(2)若直线不经过第四象限,求k的取值范围;
(3)若直线l交x轴负半轴于A,交y轴正半轴于B,△AOB的面积为S(O为坐标原点),求S的最小值并求此时直线l的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的左右焦点分别为
的左右焦点分别为![]() ,
,![]() 是椭圆短轴的一个顶点,且
是椭圆短轴的一个顶点,且![]() 是面积为
是面积为![]() 的等腰直角三角形.
的等腰直角三角形.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)已知直线![]() :
:![]() 与椭圆
与椭圆![]() 交于不同的
交于不同的![]() ,
,![]() 两点,若椭圆
两点,若椭圆![]() 上存在点
上存在点![]() ,使得四边形
,使得四边形![]() 恰好为平行四边形,求直线
恰好为平行四边形,求直线![]() 与坐标轴围成的三角形面积的最小值.
与坐标轴围成的三角形面积的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】继空气净化器之后,某商品成为人们抗雾霾的有力手段,根据该商品厂提供的数据,从2015年到2018年,购买该商品的人数直线上升,根据统计图, 说法错误的是( )
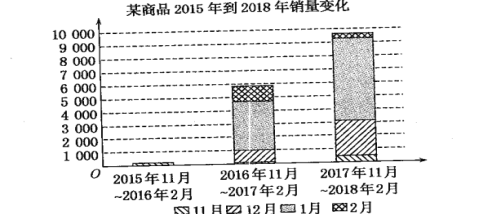
A. 连续3年,该商品在1月的销售量增长显著。
B. 2017年11月到2018年2月销量最多。
C. 从统计图上可以看出,2017年该商品总销量不超过6000台。
D. 2018年2月比2017年2月该商品总销量少。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市一次全市高中男生身高统计调查数据显示:全市100000名男生的身高服从正态分布N(168,16).现从某学校高三年级男生中随机抽取50名测量身高,测量发现被测学生身高全部介于160 cm和184 cm之间,将测量结果按如下方式分成6组:第1组[160,164),第2组[164,168),…,第6组[180,184],如图是按上述分组方法得到的频率分布直方图.
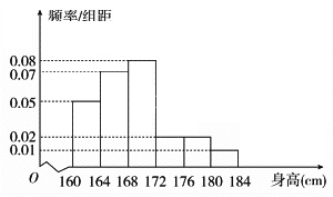
(1)由频率分布直方图估计该校高三年级男生平均身高状况;
(2)求这50名男生身高在172 cm以上(含172 cm)的人数;
(3)在这50名男生身高在172 cm以上(含172 cm)的人中任意抽取2人,将该2人中身高排名(从高到低)在全市前130名的人数记为ξ,求ξ的数学期望.
参考数据:若ξ~N(μ,σ2),则P(μ-σ<ξ≤μ+σ)=0.6826,P(μ-2σ<ξ≤μ+2σ)=0.9544,P(μ-3σ<ξ≤μ+3σ)=0.9974.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】现采用随机模拟的方法估计某运动员射击4次,至少击中3次的概率:先由计算器给出0到9之间取整数值的随机数,指定0,1表示没有击中目标,2,3,4,5,6,7, 8,9表示击中目标,以4个随机数为一组,代表射击4次的结果,经随机模拟产生了 20组随机数:
7527 0293 7140 9857 0347 4373 8636 6947 1417 4698
0371 6233 2616 8045 6011 3661 9597 7424 7610 4281
根据以上数据估计该射击运动员射击4次至少击中3次的概率为__________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校学生社团组织活动丰富,学生会为了解同学对社团活动的满意程度,随机选取了100位同学进行问卷调查,并将问卷中的这100人根据其满意度评分值(百分制)按照[40,50),[50,60),[60,70),…,[90,100]分成6组,制成如图所示频率分布直方图.
(1)求图中x的值;
(2)求这组数据的中位数;
(3)现从被调查的问卷满意度评分值在[60,80)的学生中按分层抽样的方法抽取5人进行座谈了解,再从这5人中随机抽取2人作主题发言,求抽取的2人恰在同一组的概率.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com