设函数f（x）＝a（x＋
）＋2lnx，g（x）＝
．
（Ⅰ）若a>0且a≠2，直线l与函数f（x）和函数g（x）的图象相切于一点，求切线l的方程．
（Ⅱ）若f（x）在[2，4]内为单调函数，求实数a的取值范围；
解：（Ⅰ）∵
=
，∴
因为直线
与函数
的图象相切于同一点
……………………………………………………………4分
解得
(
)，（
舍去）
,
;
,
,
;
,
①当
时，则的方程为:
②当
时，又因为点（
也在
有
即
令
，
易得方程在
一定有解
所以的方程为
综上所述直线的方程为或………………6分
（Ⅱ）∵=
要使在[2,4]为单调增函数，须
在[2,4]恒成立，
即
在[2,4]恒成立，即
在[2,4]恒成立，
又
即
(
) ……………………8分
设
(),因为
(
)所以
在
)上单调递减.
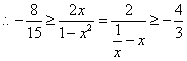
所以当
时，在[2,4]为单调增函数；………………………………10分
同理要使为单调减函数，须
在[2,4]恒成立，
易得
综上，若在[2,4]为单调函数，则
的取值范围为或…12分
科目：高中数学 来源： 题型：
设函数f（x）＝a·b，其中向量a＝（cos
，sin），（x∈R），向量b＝（cosj，sinj)
（Ⅰ）求j的值；
（Ⅱ）若函数y＝1＋sin的图象按向量c＝（m，n） （| m |＜p)平移可得到函数
y＝f（x）的图象，求向量c．
查看答案和解析>>
科目：高中数学 来源：2014届河南省原名校联盟高三上学期第一次摸底考试理科数学试卷（解析版） 题型：解答题
设函数f（x）＝
－sin（2x－
）．
（1）求函数f（x）的最大值和最小值；
（2）△ABC的内角A，B，C的对边分别为a，b，c，c＝3，f（
）＝
，若sinB＝2sinA，求△ABC的面积．
查看答案和解析>>
科目：高中数学 来源：2012-2013学年河南省郑州市高三第十三次调考理科数学试卷（解析版） 题型：选择题
设函数f（x）＝
－lnx，则y＝f（x）
A．在区间（
，1），（1，e）内均有零点
B．在区间（，1），（1，e）内均无零点
C．在区间（，1）内有零点，在区间（1，e）内无零点
D．在区间（，1）内无零点，在区间（1，e）内有零点
查看答案和解析>>
科目：高中数学 来源：2014届北京市高一上学期期中考试数学AP班 题型：选择题
设函数f（x）＝a
（a>0），且f（2）＝4，则
A. f（－1）>f（－2） B. f（1）>f（2）
C. f（2）<f（－2） D.f（－3）>f（－2）
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com