证明:证法一: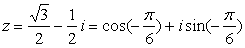
ω=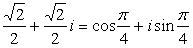
于是zω=cos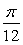 +isin +isin , , =cos(- =cos(-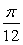 )+isin(- )+isin(-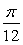 ). ).
z2ω3=[cos(-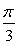 )+isin(- )+isin(-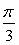 )]×(cos )]×(cos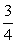 π+isin π+isin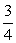 π)=cos π)=cos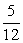 π+isin π+isin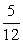 π π
因为OP与OQ的夹角为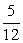 π-(- π-(-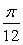 )= )=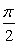 . .
所以OP⊥OQ
又因为|OP|=|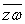 |=1,|OQ|=|z2ω3|=|z|2|ω|3=1 |=1,|OQ|=|z2ω3|=|z|2|ω|3=1
∴|OP|=|OQ|.
由此知△OPQ为等腰直角三角形.
证法二:∵z=cos(-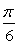 )+isin(- )+isin(-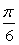 ). ).
∴z3=-i
又ω=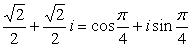 . .
∴ω4=-1
于是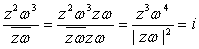
由此得OP⊥OQ,|OP|=|OQ|
故△OPQ为等腰直角三角形.
| 
 阅读快车系列答案
阅读快车系列答案