
已知关于x的实系数二次方程x2+ax+b=0有两实根α、β,证明:
①如果|α|<2,|β|<2,则2|a|<4+b且|b|<4;
②如果2|a|<4+b且|b|<4,则|α|<2,|β|<2.
证明:(1)∵|α|<2,|β|<2,由韦达定理, ∴|b|=|αβ|=|α|·|β|<4. 设f(x)=x2+ax+b,如图,抛物线开口向上,又|α|<2,|β|<2, ∴ ∴-(4+b)<2a<4+b (2)由2|a|<4+b得4+2a+b>0, 即f(2)>0; ① 且4-2a+b>0, ② 即f(-2)>0. 由此可知,f(x)=0的每个实根或者在-2与2之间,或者在-2与2之外. 1)若两根α,β均在-2与2之外,则与|b|=|αβ|<4相矛盾. 2)若α(或β)在-2与2之外,由于|b|=|αβ|<4,则另一根β(或α)必须落在-2与2之间. ∴f(-2)<0(或f(2)<0),这与①、②式矛盾. 综上所述,α,β必须落在-2与2之间. ∴|α|<2,|β|<2.
|


科目:高中数学 来源: 题型:
| b | i |
查看答案和解析>>
科目:高中数学 来源:2012-2013学年江苏省常州高级中学高三(上)期中数学试卷(理科)(解析版) 题型:填空题
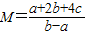 的最小值是 .
的最小值是 .查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com