
| 选手 | 甲 | 乙 | 丙 | ||
| 概率 |
| p | P |
科目:高中数学 来源:不详 题型:解答题
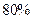 ,计算(结果保留到小数点后面第2位)
,计算(结果保留到小数点后面第2位)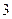 次预报准确的概率
次预报准确的概率查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 装置就可以正常工作。每套系统都由三种电子模块T1,T2,T3组成(如图所示已知T1,T2,T3正常工作的概率都是
装置就可以正常工作。每套系统都由三种电子模块T1,T2,T3组成(如图所示已知T1,T2,T3正常工作的概率都是 ,且T1,T2,T3能否正常工作相互独立.(注:对每一套系统或每一种电子模块而言,只要有电流通过就能正常工作.)
,且T1,T2,T3能否正常工作相互独立.(注:对每一套系统或每一种电子模块而言,只要有电流通过就能正常工作.)
 ;
; ,求
,求 的分布列和期望.
的分布列和期望.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 ,乙获胜的概率为
,乙获胜的概率为 .如果将“乙获得冠军”的事件称为“爆出冷门”.试求此项赛事爆出冷门的概率.
.如果将“乙获得冠军”的事件称为“爆出冷门”.试求此项赛事爆出冷门的概率.查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
A.
| B.
| C.
| D.
|
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
| 降水量X | 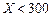 | 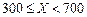 | 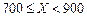 | 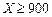 |
工期延误天数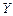 | 0 | 2 | 6 | 10 |
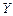 的均值与方差;(2)在降水量X至少是300的条件下,工期延误不超过6天的概率.
的均值与方差;(2)在降水量X至少是300的条件下,工期延误不超过6天的概率.查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
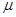 ,
,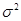 )的随机变量在区间(
)的随机变量在区间(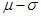 ,
,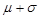 ),(
),(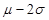 ,
,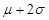 ),和(
),和(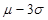 ,
,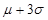 )内取值的概率分别为68.3%,95.4%,和99.7%.某校为高一年级1000名新生每人定制一套校服,经统计,学生的身高(单位:cm)服从正态分布(165,52),则适合身高在155~175cm范围内的校服大约要定制( )
)内取值的概率分别为68.3%,95.4%,和99.7%.某校为高一年级1000名新生每人定制一套校服,经统计,学生的身高(单位:cm)服从正态分布(165,52),则适合身高在155~175cm范围内的校服大约要定制( )| A.683套 | B.954套 | C.972套 | D.997套 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com