
【题目】已知函数f(x)=lnx﹣x+ ![]() +1(a∈R).
+1(a∈R).
(1)讨论f(x)的单调性与极值点的个数;
(2)当a=0时,关于x的方程f(x)=m(m∈R)有2个不同的实数根x1 , x2 , 证明:x1+x2>2.
【答案】
(1)解:解:f′(x)= ![]() ﹣1﹣
﹣1﹣ ![]() =
= ![]() ,x>0
,x>0
方程﹣x2+x﹣a=0的判别式为△=1﹣4a,
①当a≥ ![]() 时,f′(x)≤0,f(x)在(0,+∞),为减函数,无极值点,
时,f′(x)≤0,f(x)在(0,+∞),为减函数,无极值点,
②当0≤a< ![]() 时,令f′(x)=0,解得x1=
时,令f′(x)=0,解得x1= ![]() >0,x2=
>0,x2= ![]() ,
,
当f′(x)<0,解得0<x< ![]() ,x>
,x> ![]() ,
,
此时f(x)在(0, ![]() ),(
),( ![]() ,+∞)为减函数,
,+∞)为减函数,
当f′(x)>0时,解得 ![]() <x<
<x< ![]() ,
,
此时f(x)在( ![]() ,
, ![]() )为增函数,
)为增函数,
此时f(x)有一个极大值点x= ![]() ,和一个极小值点x=
,和一个极小值点x= ![]() ,
,
③当a<0,令f′(x)=0,解得x1= ![]() <0,x2=
<0,x2= ![]() >0,
>0,
当f′(x)>0,解得0<x< ![]() ,此时f(x)在(0,
,此时f(x)在(0, ![]() ),为增函数,
),为增函数,
当f′(x)<0时,解得x> ![]() ,此时在(
,此时在( ![]() ,+∞)为减函数,
,+∞)为减函数,
此时f(x)有一个极大值点x= ![]()
(2)由题意知f(x1)=m,f(x2)=m,
故f(x1)=f(x2),
∵x1≠x2,不妨设x1<x2,
∴lnx1﹣x1+1=lnx2﹣x2+1,
∴ln ![]() =x2﹣x1,
=x2﹣x1,
令 ![]() =t,则x2=tx1,
=t,则x2=tx1,
∴lnt=(t﹣1)x1,
∴x1= ![]() ,x2=tx1=
,x2=tx1= ![]() ,
,
故要证x1+x2= ![]() lnt>2,t>1,
lnt>2,t>1,
即证(t+1)lnt>2(t﹣1),
令g(t)=(t+1)lnt﹣2t+2,
∴g′(t)= ![]() +lnt﹣2=
+lnt﹣2= ![]() ,
,
令h(t)=tlnt﹣t+1,t>1,
则h′(t)=lnt>0,
∴h(t)在t∈(1,+∞)上为增函数,
∴h(t)>h(1)=0,
∴g(t)在(1,+∞)为增函数,
∴g(t)>g(1)=0,
∴(t+1)lnt>2(t﹣1),
即 ![]() lnt>2,
lnt>2,
∴x1+x2>2
【解析】(1)先求出导函数,再根据判别式和a的范围分类讨论,即可判断函数的单调性和极值点的个数,(2)问题转化为要证x1+x2= ![]() lnt>2,t>1,即证(t+1)lnt>2(t﹣1),构造函数,根据导数和函数的单调性和最值得关系即可证明.
lnt>2,t>1,即证(t+1)lnt>2(t﹣1),构造函数,根据导数和函数的单调性和最值得关系即可证明.
【考点精析】解答此题的关键在于理解利用导数研究函数的单调性的相关知识,掌握一般的,函数的单调性与其导数的正负有如下关系: 在某个区间![]() 内,(1)如果
内,(1)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递增;(2)如果
在这个区间单调递增;(2)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递减,以及对函数的极值与导数的理解,了解求函数
在这个区间单调递减,以及对函数的极值与导数的理解,了解求函数![]() 的极值的方法是:(1)如果在
的极值的方法是:(1)如果在![]() 附近的左侧
附近的左侧![]() ,右侧
,右侧![]() ,那么
,那么![]() 是极大值(2)如果在
是极大值(2)如果在![]() 附近的左侧
附近的左侧![]() ,右侧
,右侧![]() ,那么
,那么![]() 是极小值.
是极小值.


 每课必练系列答案
每课必练系列答案科目:高中数学 来源: 题型:
【题目】如图,四棱锥P﹣ABCD的底面为矩形,侧棱PA⊥底面ABCD,且PA=AD,E,F分别是线段PA,PD的中点,H在线段AB上.
(1)求证:PC⊥AF;
(2)若平面PBC∥平面EFH,求证H是AB的中点;
(3)若AD=4,AB=2,求点D到平面PAC的距离.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,斜三棱柱ABC﹣A1B1C1的侧面AA1C1C是菱形,侧面ABB1A1⊥侧面AA1C1C,A1B=AB=AA1=2,△AA1C1的面积为 ![]() ,且∠AA1C1为锐角.
,且∠AA1C1为锐角.
(I) 求证:AA1⊥BC1;
(Ⅱ)求锐二面角B﹣AC﹣C1的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知四棱锥P﹣ABCD中,底面ABCD是直角梯形,∠ADC=90°,AB∥CD,AD=DC= ![]() AB=
AB= ![]() ,平面PBC⊥平面ABCD.
,平面PBC⊥平面ABCD. 
(1)求证:AC⊥PB;
(2)若PB=PC= ![]() ,问在侧棱PB上是否存在一点M,使得二面角M﹣AD﹣B的余弦值为
,问在侧棱PB上是否存在一点M,使得二面角M﹣AD﹣B的余弦值为 ![]() ?若存在,求出
?若存在,求出 ![]() 的值;若不存在,说明理由.
的值;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示的程序框图的算法思路源于我国古代数学中的秦九韶算法,执行该程序框图,则输出的结果S表示的值为( ) 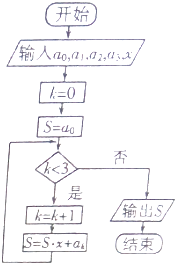
A.a0+a1+a2+a3
B.(a0+a1+a2+a3)x3
C.a0+a1x+a2x2+a3x3
D.a0x3+a1x2+a2x+a3
查看答案和解析>>
科目:高中数学 来源: 题型:
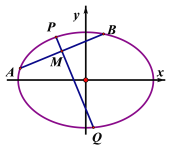
【题目】已知椭圆 ![]() 的焦距为
的焦距为 ![]() ,且过点
,且过点 ![]() ,设
,设 ![]() ,
,![]() 是
是 ![]() 上的两个动点,线段
上的两个动点,线段 ![]() 的中点
的中点 ![]() 的横坐标为
的横坐标为 ![]() ,线段
,线段 ![]() 的中垂线交椭圆
的中垂线交椭圆 ![]() 于
于 ![]() ,
,![]() 两点.
两点.
(1)求椭圆 ![]() 的方程;
的方程;
(2)设![]() 点纵坐标为m,求直线
点纵坐标为m,求直线![]() 的方程,并求出
的方程,并求出 ![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若直角坐标平面内两点P,Q满足条件:①P、Q都在函数y=f(x)的图象上;②P、Q关于原点对称,则对称点(P,Q)是函数y=f(x)的一个“伙伴点组”(点对(P,Q)与(Q,P)看作同一个“伙伴点组”).则下列函数中,恰有两个“伙伴点组”的函数是(填空写所有正确选项的序号)
①y= ![]() ;②y=
;②y=  ;③y=
;③y= ![]() ;④y=
;④y=  .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com