
【题目】已知f(x)=x-![]() (a>0),g(x)=2lnx+bx且直线y=2x-2与曲线y=g(x)相切.
(a>0),g(x)=2lnx+bx且直线y=2x-2与曲线y=g(x)相切.
(1)若对[1,+![]() )内的一切实数x,小等式f(x)≥g(x)恒成立,求实数a的取值范围;
)内的一切实数x,小等式f(x)≥g(x)恒成立,求实数a的取值范围;
(2)当a=l时,求最大的正整数k,使得对[e,3](e=2.71828是自然对数的底数)内的任意k个实数x1,x2,,xk都有![]() 成立;
成立;
(3)求证:![]() .
.
【答案】(1)![]() ;(2)
;(2)![]() 的最大值为
的最大值为![]() .(3)见解析.
.(3)见解析.
【解析】
试题(1)设点![]() 为直线
为直线![]() 与曲线
与曲线![]() 的切点,则有
的切点,则有![]() . (*)
. (*)
![]() ,
,![]() . (**)
. (**)
由(*)、(**)两式,解得![]() ,
,![]() .
.
由![]() 整理,得
整理,得![]() ,
,
![]() ,
,![]() 要使不等式
要使不等式![]() 恒成立,必须
恒成立,必须![]() 恒成立.
恒成立.
设![]() ,
,![]() ,
,
![]() ,
,![]() 当
当![]() 时,
时,![]() ,则
,则![]() 是增函数,
是增函数,
![]() ,
,![]() 是增函数,
是增函数,![]() ,
,![]()
因此,实数![]() 的取值范围是
的取值范围是![]() .
.
(2)当![]() 时,
时,![]() ,
,
![]() ,
,![]() 在
在![]() 上是增函数,
上是增函数,![]() 在
在![]() 上的最大值为
上的最大值为![]() .
.
要对![]() 内的任意
内的任意![]() 个实数
个实数![]() 都有
都有![]()
成立,必须使得不等式左边的最大值小于或等于右边的最小值,
![]() 当
当![]() 时不等式左边取得最大值,
时不等式左边取得最大值,![]() 时不等式右边取得最小值.
时不等式右边取得最小值.
![]() ,解得
,解得![]() .
.
因此,![]() 的最大值为
的最大值为![]() .
.
(3)证明(法一):当![]() 时,根据(1)的推导有,
时,根据(1)的推导有,![]() 时,
时,![]() ,
,
即![]() .
.
令![]() ,得
,得![]() ,
,
化简得![]() ,
,
![]() .
.
(法二)数学归纳法:当![]() 时,左边=
时,左边=![]() ,右边=
,右边=![]() ,
,
根据(1)的推导有,![]() 时,
时,![]() ,即
,即![]() .
.
令![]() ,得
,得![]() ,即
,即![]() .
.
因此,![]() 时不等式成立.
时不等式成立.
(另解:![]() ,
,![]() ,
,![]() ,即
,即![]() .)
.)
假设当![]() 时不等式成立,即
时不等式成立,即![]() ,
,
则当![]() 时,
时,![]() ,
,
要证![]() 时命题成立,即证
时命题成立,即证![]() ,
,
即证![]() .
.
在不等式![]() 中,令
中,令![]() ,得
,得
![]() .
.
![]() 时命题也成立.
时命题也成立.
根据数学归纳法,可得不等式![]() 对一切
对一切![]() 成立.
成立.


 浙大优学小学年级衔接捷径浙江大学出版社系列答案
浙大优学小学年级衔接捷径浙江大学出版社系列答案科目:高中数学 来源: 题型:
【题目】“微信运动”是手机![]() 推出的多款健康运动软件中的一款,大学生
推出的多款健康运动软件中的一款,大学生![]() 的微信好友中有400位好友参与了“微信运动”.他随机抽取了40位参与“微信运动”的微信好友(女20人,男20人)在某天的走路步数,经统计,其中女性好友走路的步数情况可分为五个类别:
的微信好友中有400位好友参与了“微信运动”.他随机抽取了40位参与“微信运动”的微信好友(女20人,男20人)在某天的走路步数,经统计,其中女性好友走路的步数情况可分为五个类别:![]() 、0~2000步,(说明:“0~2000”表示“大于或等于0,小于2000”,以下同理),
、0~2000步,(说明:“0~2000”表示“大于或等于0,小于2000”,以下同理),![]() 、2000~5000步,
、2000~5000步,![]() 、5000~8000步,
、5000~8000步,![]() 、8000~10000步,
、8000~10000步,![]() 、10000~12000步,且
、10000~12000步,且![]() 三种类别的人数比例为
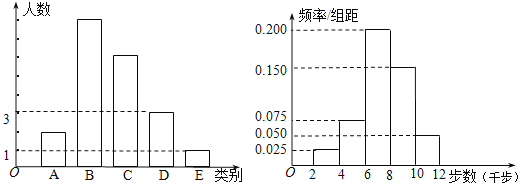
三种类别的人数比例为![]() ,将统计结果绘制如图所示的柱形图;男性好友走路的步数数据绘制如图所示的频率分布直方图.
,将统计结果绘制如图所示的柱形图;男性好友走路的步数数据绘制如图所示的频率分布直方图.
参与者 | 超越者 | 合计 | |
男 | 20 | ||
女 | 20 | ||
合计 | 40 |
若某人一天的走路步数大于或等于8000,则被系统认定为“超越者”,否则被系统认定为“参与者”.
(Ⅰ)若以大学生![]() 抽取的微信好友在该天行走步数的频率分布,作为参与“微信运动”的所有微信好友每天走路步数的概率分布,试估计大学生
抽取的微信好友在该天行走步数的频率分布,作为参与“微信运动”的所有微信好友每天走路步数的概率分布,试估计大学生![]() 的参与“微信运动”的400位微信好友中,每天走路步数在
的参与“微信运动”的400位微信好友中,每天走路步数在
(Ⅱ)若在大学生![]() 该天抽取的步数在8000~12000的微信好友中,按男女比例分层抽取9人进行身体状况调查,然后再从这9位微信好友中随机抽取4人进行采访,求其中至少有一位女性微信好友被采访的概率;
该天抽取的步数在8000~12000的微信好友中,按男女比例分层抽取9人进行身体状况调查,然后再从这9位微信好友中随机抽取4人进行采访,求其中至少有一位女性微信好友被采访的概率;
(Ⅲ)请根据抽取的样本数据完成下面的![]() 列联表,并据此判断能否有
列联表,并据此判断能否有![]() 的把握认为“认定类别”与“性别”有关?
的把握认为“认定类别”与“性别”有关?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了改善空气质量,某市规定,从2018年1月1日起,对二氧化碳排放量超过![]() 的轻型汽车进行惩罚性征税.检测单位对甲乙两品牌轻型汽车各抽取5辆进行二氧化碳排放量检测,记录如下:(单位:
的轻型汽车进行惩罚性征税.检测单位对甲乙两品牌轻型汽车各抽取5辆进行二氧化碳排放量检测,记录如下:(单位:![]() )
)
甲 | 80 | 110 | 120 | 140 | 150 |
乙 | 100 | 120 |
| 100 | 160 |
经测算得乙品牌轻型汽车二氧化碳排放量的平均值为![]() .
.
(1)求表中![]() 的值,并比较甲乙两品牌轻型汽车二氧化碳排放量的稳定性;
的值,并比较甲乙两品牌轻型汽车二氧化碳排放量的稳定性;
(2)从被检测的5辆甲品牌汽车中随机抽取2辆,求至少有1辆二氧化碳排放量超过![]() 的概率.(注:方差
的概率.(注:方差![]() ,其中
,其中![]() 为
为![]() 的平均数).
的平均数).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知某运动员每次投篮命中的概率都是40%.现采用随机模拟的方法估计该运动员三次投篮恰有一次命中的概率:先由计算器产生0到9之间取整数值的随机数,指定1,2,3,4表示命中,5,6,7,8,9,0表示不命中;再以每三个随机数作为一组,代表三次投篮的结果.经随机模拟产生了如下20组随机数:907,966,191,925,271,932,812,458,569,683,431,257,393,027,556,488,730,113,537,989.据此估计,该运动员三次投篮恰有两次命中的概率为( )
A.0.25B.0.2C.0.35D.0.4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市约有20万住户,为了节约能源,拟出台“阶梯电价”制度,即制定住户月用电量的临界值![]() ,若某住户某月用电量不超过
,若某住户某月用电量不超过![]() 度,则按平价(即原价)0.5(单位:元/度)计费;若某月用电量超过
度,则按平价(即原价)0.5(单位:元/度)计费;若某月用电量超过![]() 度,则超出部分按议价
度,则超出部分按议价![]() (单位:元/度)计费,未超出部分按平价计费.为确定
(单位:元/度)计费,未超出部分按平价计费.为确定![]() 的值,随机调查了该市100户的月用电量,统计分析后得到如图所示的频率分布直方图.根据频率分布直方图解答以下问题(同一组数据用该区间的中点值作代表).
的值,随机调查了该市100户的月用电量,统计分析后得到如图所示的频率分布直方图.根据频率分布直方图解答以下问题(同一组数据用该区间的中点值作代表).
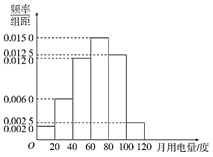
(1)若该市计划让全市![]() 的住户在“阶梯电价”出台前后缴纳的电费不变,求临界值
的住户在“阶梯电价”出台前后缴纳的电费不变,求临界值![]() ;
;
(2)在(1)的条件下,假定出台“阶梯电价”之后,月用电量未达![]() 度的住户用电量保持不变;月用电量超过
度的住户用电量保持不变;月用电量超过![]() 度的住户节省“超出部分”的
度的住户节省“超出部分”的![]() ,试估计全市每月节约的电量;
,试估计全市每月节约的电量;
(3)在(1)(2)条件下,若出台“阶梯电价”前后全市缴纳电费总额不变,求议价![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】过点![]() 作圆
作圆![]() 的两条切线,切点分别为
的两条切线,切点分别为![]() 、
、![]() ,给出下列四个结论:
,给出下列四个结论:
①![]() ;
;
②若![]() 为直角三角形,则
为直角三角形,则![]() ;
;
③![]() 外接圆的方程为
外接圆的方程为![]() ;
;
④直线![]() 的方程为
的方程为![]() .
.
其中所有正确结论的序号为( )
A.②④B.③④C.②③D.①②④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() ,
,![]() 为两非零有理数列(即对任意的
为两非零有理数列(即对任意的![]() ,
,![]() 均为有理数),
均为有理数),![]() 为一无理数列(即对任意的
为一无理数列(即对任意的![]() ,
,![]() 为无理数).
为无理数).
(1)已知![]() ,并且
,并且![]() 对任意的
对任意的![]() 恒成立,试求
恒成立,试求![]() 的通项公式.
的通项公式.
(2)若![]() 为有理数列,试证明:对任意的
为有理数列,试证明:对任意的![]() ,
,![]() 恒成立的充要条件为
恒成立的充要条件为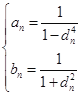 .
.
(3)已知![]() ,
,![]() ,对任意的
,对任意的![]() ,
,![]() 恒成立,试计算
恒成立,试计算![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com