
ΓΨΧβΡΩΓΩΈΣΚκ―ο÷–ΜΣ”≈–ψ¥ΪΆ≥ΈΡΜ·Θ§Ρ≥÷–―ßΗΏ»ΐΡξΦΕάϊ”ΟΩΈ”ύ ±ΦδΉι÷·―ß…ζΩΣ’Ι–Γ–Ά÷Σ ΕΨΚ»ϋΘ°±»»ϋΙφ‘ρΘΚΟΩΗω≤Έ»ϋ’ΏΜΊ¥πAΓΔBΝΫΉιΧβΡΩΘ§ΟΩΉιΧβΡΩΗς”–ΝΫΒάΧβΘ§ΟΩΒάΧβ¥πΕ‘ΒΟ1Ζ÷Θ§¥π¥μΒΟ0Ζ÷Θ§ΝΫΉιΧβΡΩΒΟΖ÷ΒΡΚΆΉωΈΣΗΟ―Γ ÷ΒΡ±»»ϋ≥…Φ®Θ°–ΓΟςΙάΦΤ¥πΕ‘AΉιΟΩΒάΧβΒΡΗ≈¬ ΨυΈΣ![]() Θ§¥πΕ‘BΉιΟΩΒάΧβΒΡΗ≈¬ ΨυΈΣ
Θ§¥πΕ‘BΉιΟΩΒάΧβΒΡΗ≈¬ ΨυΈΣ![]() Θ°
Θ°
Θ®ΔώΘ©Α¥¥ΥΙάΦΤ«σ–ΓΟςAΉιΧβΒΟΖ÷±»BΉιΧβΒΟΖ÷Εύ1Ζ÷ΒΡΗ≈¬ ΘΜ
Θ®ΔρΘ©Φ«–ΓΟς‘Ύ±»»ϋ÷–ΒΡΒΟΖ÷ΈΣΠΈΘ§Α¥¥ΥΙάΦΤΠΈΒΡΖ÷≤ΦΝ–ΚΆ ΐ―ßΤΎΆϊEΠΈΘ°
ΓΨ¥πΑΗΓΩΘ®ΔώΘ©![]() ΘΜΘ®ΔρΘ©Ζ÷≤ΦΝ–ΦϊœξΫβΘ§
ΘΜΘ®ΔρΘ©Ζ÷≤ΦΝ–ΦϊœξΫβΘ§![]()
ΓΨΫβΈωΓΩ
Θ®1Θ©Ζ÷Έω¬ζΉψΧβ“βΒΡ ¬ΦΰΘ§»ΜΚσΖ÷±πΦΤΥψ≥ωΗ≈¬ Θ§‘Ό”ΟΗ≈¬ Φ”Ζ®ΙΪ ΫΦΤΥψΦ¥Ω…ΘΜ
Θ®2Θ©œ»ΗυΨίΧβ“β«σΒΟΠΈΩ…»ΓΒΡ÷ΒΘ§‘ΌΗυΨίΧβ“βΘ§Ζ÷±π«σ≥ωΗ≈¬ Θ§Ά®ΙΐΖ÷≤ΦΝ–ΦΤΥψ ΐ―ßΤΎΆϊΦ¥Ω….
Θ®ΔώΘ©…η–ΓΟςAΉιΧβΒΟ1Ζ÷Θ§BΉιΧβΒΟ0Ζ÷ΈΣ ¬ΦΰMΘ§
AΉιΧβΒΟ2Ζ÷Θ§BΉιΧβΒΟ1Ζ÷ΈΣ ¬ΦΰNΘ§
‘ρ–ΓΟςAΉιΧβΒΟΖ÷±»BΉιΧβΒΟΖ÷Εύ1Ζ÷ΒΡΗ≈¬ ΘΚ
PΘ®MΓ»NΘ©ΘΫPΘ®MΘ©+PΘ®NΘ©
![]()
![]() Θ°
Θ°
Θ®ΔρΘ©”…Χβ“β–ΓΟς‘Ύ±»»ϋ÷–ΒΡΒΟΖ÷ΠΈΒΡΩ…Ρή»Γ÷ΒΈΣ0Θ§1Θ§2Θ§3Θ§4Θ®ΒΞΈΜΘΚΖ÷Θ©
‘ρPΘ®ΠΈΘΫ0Θ©ΘΫΘ®1![]() Θ©2Θ®1
Θ©2Θ®1![]() Θ©2
Θ©2![]() Θ§
Θ§
PΘ®ΠΈΘΫ1Θ©![]() Θ§
Θ§
PΘ®ΠΈΘΫ2Θ©![]() Θ§
Θ§
PΘ®ΠΈΘΫ3Θ©![]() Θ§
Θ§
PΘ®ΠΈΘΫ4Θ©ΘΫΘ®![]() Θ©2Θ®
Θ©2Θ®![]() Θ©2
Θ©2![]() Θ§
Θ§
ΓύΠΈΒΡΖ÷≤ΦΝ–ΈΣΘΚ
ΠΈ | 0 | 1 | 2 | 3 | 4 |
P |
|
|
|
|
|
EΠΈ![]() Θ°
Θ°


 Ά§≤ΫΝΖœΑ«ΩΜ·ΆΊ’ΙœΒΝ–¥πΑΗ
Ά§≤ΫΝΖœΑ«ΩΜ·ΆΊ’ΙœΒΝ–¥πΑΗ
| ΡξΦΕ | ΗΏ÷–ΩΈ≥Χ | ΡξΦΕ | ≥θ÷–ΩΈ≥Χ |
| ΗΏ“Μ | ΗΏ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ“Μ | ≥θ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏΕΰ | ΗΏΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θΕΰ | ≥θΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏ»ΐ | ΗΏ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ»ΐ | ≥θ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ…ηΦ·Κœ![]() ±μ ΨΨΏ”–œ¬Ν––‘÷ ΒΡΚ· ΐ
±μ ΨΨΏ”–œ¬Ν––‘÷ ΒΡΚ· ΐ![]() ΒΡΦ·ΚœΘΚΔΌ
ΒΡΦ·ΚœΘΚΔΌ![]() ΒΡΕ®“ε”ρΈΣ
ΒΡΕ®“ε”ρΈΣ![]() ΘΜΔΎΕ‘»Έ“β
ΘΜΔΎΕ‘»Έ“β![]() Θ§ΕΦ”–
Θ§ΕΦ”–![]()
Θ®1Θ©»τΚ· ΐ![]() Θ§÷ΛΟς
Θ§÷ΛΟς![]() «ΤφΚ· ΐΘΜ≤ΔΒ±
«ΤφΚ· ΐΘΜ≤ΔΒ±![]() Θ§
Θ§![]() Θ§«σ
Θ§«σ![]() Θ§
Θ§![]() ΒΡ÷ΒΘΜ
ΒΡ÷ΒΘΜ
Θ®2Θ©…ηΚ· ΐ![]() Θ®aΈΣ≥Θ ΐΘ© «ΤφΚ· ΐΘ§≈–Εœ
Θ®aΈΣ≥Θ ΐΘ© «ΤφΚ· ΐΘ§≈–Εœ![]() «Ζώ τ”Ύ
«Ζώ τ”Ύ![]() Θ§≤ΔΥΒΟςάμ”…ΘΜ
Θ§≤ΔΥΒΟςάμ”…ΘΜ
Θ®3Θ©‘ΎΘ®2Θ©ΒΡΧθΦΰœ¬Θ§»τ Θ§Χ÷¬έΚ· ΐ
Θ§Χ÷¬έΚ· ΐ![]() ΒΡΝψΒψΗω ΐ.
ΒΡΝψΒψΗω ΐ.
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ”…ΙυΖΪ÷¥ΒΦΈβΨ©÷ς―ίΒΡΒγ”ΑΓΕΝςάΥΒΊ«ρΓΖ”Ύ2019Ρξ2‘¬5»’Τπ‘Ύ÷–ΙζΡΎΒΊ…œ”≥Θ§”ΑΤ§“ΐΖΔΝΥΙέ”Α»»≥±Θ§‘ΛΦΤΓΕΝςάΥΒΊ«ρΓΖΤ±ΖΩ ’»κ47“Ύ»ΥΟώ±“Θ§≥§ΙΐΓΕΚλΚΘ––Ε·ΓΖ≥…ΈΣ÷–Ιζ”Α ΖΤ±ΖΩ―«ΨϋΘ§Ϋω¥Έ”ΎΓΕ’Ϋά«2ΓΖ.Ρ≥Βγ”Α‘ΚΈΣΝΥΫβΗΟ”Α‘ΚΙέΩ¥ΓΕΝςάΥΒΊ«ρΓΖΒΡΙέ÷ΎΒΡΡξΝδΙΙ≥…«ιΩωΘ§ΥφΜζ≥ι»ΓΝΥ40ΟϊΙέ÷ΎΘ§ΫΪΥϊΟ«ΒΡΡξΝδΖ÷≥…7ΕΈΘΚ![]() Θ§
Θ§![]() Θ§
Θ§![]() Θ§
Θ§![]() Θ§
Θ§![]() Θ§
Θ§![]() Θ§
Θ§![]() Θ§ΒΟΒΫ»γΆΦΥυ ΨΒΡΤΒ¬ Ζ÷≤Φ÷±ΖΫΆΦ.
Θ§ΒΟΒΫ»γΆΦΥυ ΨΒΡΤΒ¬ Ζ÷≤Φ÷±ΖΫΆΦ.
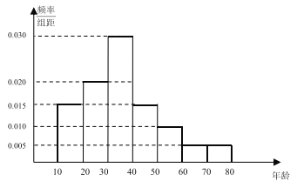
Θ®1Θ© ‘«σ’β40ΟϊΙέ÷ΎΡξΝδΒΡΤΫΨυ ΐΓΔ÷–ΈΜ ΐΓΔ÷Ύ ΐΘΜ
Θ®2Θ©Θ®iΘ©»τ¥”―υ±Ψ÷–ΡξΝδ‘Ύ50Υξ“‘…œΒΡΙέ÷Ύ÷–»Έ»Γ3Οϊ‘υΥΆVIPΙσ±ωΙέ”ΑΩ®Θ§«σ’β3ΟϊΙέ÷Ύ÷Ν…Ό”–1»ΥΡξΝδ≤ΜΒΆ”Ύ70ΥξΒΡΗ≈¬ ΘΜ
Θ®iiΘ©ΗΟΒγ”Α‘ΚΨωΕ®≤…”Ο≥ιΫ±ΖΫ Ϋά¥Χα…ΐΙέ”Α»Υ ΐΘ§ΫΪΓΕΝςάΥΒΊ«ρΓΖΒγ”ΑΤ±Τ±ΦέΧαΗΏ20‘ΣΘ§≤Δ‘ –μΙΚ¬ρΒγ”ΑΤ±ΒΡΙέ÷Ύ≥ιΫ±3¥ΈΘ§÷–Ϋ±1¥ΈΓΔ2¥ΈΓΔ3¥ΈΖ÷±πΫ±œ÷Ϋπ![]() ‘ΣΓΔ
‘ΣΓΔ![]() ‘ΣΘ§
‘ΣΘ§![]() ‘Σ.…ηΙέ÷ΎΟΩ¥Έ÷–Ϋ±ΒΡΗ≈¬ ΨυΈΣ
‘Σ.…ηΙέ÷ΎΟΩ¥Έ÷–Ϋ±ΒΡΗ≈¬ ΨυΈΣ![]() Θ§»τ“Σ Ι≥ιΫ±ΖΫΑΗΕ‘Βγ”Α‘Κ”–άϊΘ§‘ρ
Θ§»τ“Σ Ι≥ιΫ±ΖΫΑΗΕ‘Βγ”Α‘Κ”–άϊΘ§‘ρ![]() ΉνΗΏΩ…Ε®ΈΣΕύ…Ό‘ΣΘΩΘ®ΫαΙϊΨΪ»ΖΒΫΗωΈΜΘ©
ΉνΗΏΩ…Ε®ΈΣΕύ…Ό‘ΣΘΩΘ®ΫαΙϊΨΪ»ΖΒΫΗωΈΜΘ©
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩΆ÷‘≤![]() Θ®
Θ®![]() Θ©ΒΡάκ–Ρ¬ Β»”Ύ
Θ©ΒΡάκ–Ρ¬ Β»”Ύ![]() Θ§ΥϋΒΡ“ΜΗω≥Λ÷αΕΥΒψ«ΓΚΟ «≈ΉΈοœΏ
Θ§ΥϋΒΡ“ΜΗω≥Λ÷αΕΥΒψ«ΓΚΟ «≈ΉΈοœΏ![]() ΒΡΫΙΒψ.
ΒΡΫΙΒψ.
Θ®1Θ©«σΆ÷‘≤![]() ΒΡΖΫ≥ΧΘΜ
ΒΡΖΫ≥ΧΘΜ
Θ®2Θ©»τ÷±œΏ![]() ”κΆ÷‘≤
”κΆ÷‘≤![]() ”–«“÷Μ”–“ΜΗωΙΪΙ≤ΒψΘ§«“÷±œΏ
”–«“÷Μ”–“ΜΗωΙΪΙ≤ΒψΘ§«“÷±œΏ![]() ”κ÷±œΏ
”κ÷±œΏ![]() ΚΆ
ΚΆ![]() Ζ÷±πΫΜ”Ύ
Ζ÷±πΫΜ”Ύ![]() ΝΫΒψΘ§ ‘ΧΫΨΩ“‘œΏΕΈ
ΝΫΒψΘ§ ‘ΧΫΨΩ“‘œΏΕΈ![]() ΈΣ÷±ΨΕΒΡ‘≤ «ΖώΚψΙΐΕ®ΒψΘΩ»τΚψΙΐΕ®ΒψΘ§«σ≥ωΗΟΕ®ΒψΘ§»τ≤ΜΚψΙΐΕ®ΒψΘ§«κΥΒΟςάμ”….
ΈΣ÷±ΨΕΒΡ‘≤ «ΖώΚψΙΐΕ®ΒψΘΩ»τΚψΙΐΕ®ΒψΘ§«σ≥ωΗΟΕ®ΒψΘ§»τ≤ΜΚψΙΐΕ®ΒψΘ§«κΥΒΟςάμ”….
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ…ηΚ· ΐfΘ®xΘ©ΘΫsinΘ®ΠΊx+Π’Θ©![]() cosΘ®ΠΊx+Π’Θ©Θ®ΠΊΘΨ0Θ§|Π’|
cosΘ®ΠΊx+Π’Θ©Θ®ΠΊΘΨ0Θ§|Π’|![]() Θ©ΒΡΆΦœσ”κ÷±œΏyΘΫ2ΒΡΝΫΗωœύΝΎΒΡΫΜΒψ÷°ΦδΒΡΨύάκΈΣΠ–Θ§«“fΘ®xΘ©+fΘ®©¹xΘ©ΘΫ0Θ§»τgΘ®xΘ©ΘΫsinΘ®ΠΊx+Π’Θ©Θ§‘ρΘ®ΓΓ ΓΓΘ©
Θ©ΒΡΆΦœσ”κ÷±œΏyΘΫ2ΒΡΝΫΗωœύΝΎΒΡΫΜΒψ÷°ΦδΒΡΨύάκΈΣΠ–Θ§«“fΘ®xΘ©+fΘ®©¹xΘ©ΘΫ0Θ§»τgΘ®xΘ©ΘΫsinΘ®ΠΊx+Π’Θ©Θ§‘ρΘ®ΓΓ ΓΓΘ©
A.gΘ®xΘ©‘ΎΘ®0Θ§![]() Θ©…œΒΞΒςΒί‘ωB.gΘ®xΘ©‘Ύ Θ®0Θ§
Θ©…œΒΞΒςΒί‘ωB.gΘ®xΘ©‘Ύ Θ®0Θ§![]() Θ©…œΒΞΒςΒίΦθ
Θ©…œΒΞΒςΒίΦθ
C.gΘ®xΘ©‘ΎΘ®![]() Θ§
Θ§![]() Θ©…œΒΞΒςΒί‘ωD.gΘ®xΘ©‘ΎΘ®
Θ©…œΒΞΒςΒί‘ωD.gΘ®xΘ©‘ΎΘ®![]() Θ§
Θ§![]() Θ©…œΒΞΒςΒίΦθ
Θ©…œΒΞΒςΒίΦθ
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩΉ‘2009Ρξ“‘ά¥Θ§≤ΥΡώΆχ¬γΈοΝςΚΆΧ‘±Π…Χ≥«ΥΪ °“ΜΜνΕ·“―Ψ≠ΉΏΙΐ °ΡξΘ§Ρ≥ ΐ―ß–Υ»Λ–ΓΉι ’Φ·ΝΥΫϋΈεΡξΥΪ °“ΜΒ±Χλ≤ΥΡώΆχ¬γΈοΝςΕ©ΒΞ ΐΨί»γœ¬±μ.≤Δ«“≤ι÷Σ’βΈεΡξΕ©ΒΞ ΐΒΡΤΫΨυ ΐ‘ΦΈΣ6.5“ΎΦΰ.
ΡξΖί¥ζ¬κ | 1 | 2 | 3 | 4 | 5 |
ΡξΖί | 2014 | 2015 | 2016 | 2017 | 2018 |
Ε©ΒΞ ΐ | 2.8 | 4.7 |
| 8.1 | 10.4 |
Θ®1Θ©œ÷ΖΔœ÷±μ÷–“ΜΗω ΐΨί![]() Ω¥≤Μ«εΘ§ ‘«σ≥ω±μ÷–
Ω¥≤Μ«εΘ§ ‘«σ≥ω±μ÷–![]() ΒΡ÷ΒΘ§≤ΔΗυΨί ’Φ·ΒΡ’β–© ΐΨίΚΆœ¬Ν–”–ΙΊ≤ΈΩΦ ΐΨίΥΒΟςΚ· ΐ
ΒΡ÷ΒΘ§≤ΔΗυΨί ’Φ·ΒΡ’β–© ΐΨίΚΆœ¬Ν–”–ΙΊ≤ΈΩΦ ΐΨίΥΒΟςΚ· ΐ![]() Θ§
Θ§![]() ÷–Θ§ΡΡ“ΜΗωάύ–ΆΗϋ Κœ
÷–Θ§ΡΡ“ΜΗωάύ–ΆΗϋ Κœ![]() ΙΊ”Ύ
ΙΊ”Ύ![]() ΒΡΜΊΙιΖΫ≥ΧΘΜ
ΒΡΜΊΙιΖΫ≥ΧΘΜ
Θ®2Θ©“άΨίΡψΒΡ≈–ΕœΘ§«σ![]() ΙΊ”Ύ
ΙΊ”Ύ![]() ΒΡΜΊΙιΖΫ≥ΧΘΜ
ΒΡΜΊΙιΖΫ≥ΧΘΜ
Θ®3Θ©‘Λ≤β≤ΥΡώΆχ¬γΈοΝς2019ΡξΒΡΕ©ΒΞ ΐ.
≤ΈΩΦ ΐΨίΘΚ
Ε©ΒΞ ΐ | 2.8 | 4.7 |
| 8.1 | 10.4 |
| 1.03 | 1.55 | 1.87 | 2.09 | 2.34 |
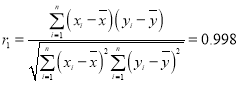 Θ§
Θ§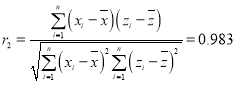 .
.
≤ΈΩΦΙΪ ΫΘΚ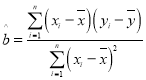 Θ§
Θ§![]() .
.
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩΕ®“εΘΚ«χΦδ![]() Θ§
Θ§![]() Θ§
Θ§![]() Θ§
Θ§![]() ΒΡ≥ΛΕ»ΨυΈΣ
ΒΡ≥ΛΕ»ΨυΈΣ![]() Θ§»τ≤ΜΒ» Ϋ
Θ§»τ≤ΜΒ» Ϋ![]() ΒΡΫβΦ· «ΜΞ≤ΜœύΫΜ«χΦδΒΡ≤ΔΦ·Θ§…ηΗΟ≤ΜΒ» ΫΒΡΫβΦ·÷–Υυ”–«χΦδΒΡ≥ΛΕ»÷°ΚΆΈΣ
ΒΡΫβΦ· «ΜΞ≤ΜœύΫΜ«χΦδΒΡ≤ΔΦ·Θ§…ηΗΟ≤ΜΒ» ΫΒΡΫβΦ·÷–Υυ”–«χΦδΒΡ≥ΛΕ»÷°ΚΆΈΣ![]() Θ§‘ρΘ® Θ©
Θ§‘ρΘ® Θ©
A. Β±![]() ±Θ§
±Θ§![]() B. Β±
B. Β±![]() ±Θ§
±Θ§![]()
C. Β±![]() ±Θ§
±Θ§![]() D. Β±
D. Β±![]() ±Θ§
±Θ§![]()
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ“―÷ΣΚ· ΐ![]() ¬ζΉψ:ΔΌΕ®“εΈΣ
¬ζΉψ:ΔΌΕ®“εΈΣ![]() ΘΜΔΎ
ΘΜΔΎ![]() .
.
Θ®1Θ©«σ![]() ΒΡΫβΈω ΫΘΜ
ΒΡΫβΈω ΫΘΜ
Θ®2Θ©»τ![]() ΘΜΨυ”–
ΘΜΨυ”–![]() ≥…ΝΔΘ§«σ
≥…ΝΔΘ§«σ![]() ΒΡ»Γ÷ΒΖΕΈßΘΜ
ΒΡ»Γ÷ΒΖΕΈßΘΜ
Θ®3Θ©…η![]() Θ§ ‘«σΖΫ≥Χ
Θ§ ‘«σΖΫ≥Χ![]() ΒΡΫβ.
ΒΡΫβ.
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ“―÷ΣΚ· ΐ![]() .
.
Θ®1Θ©Χ÷¬έ![]() ΒΡΒΞΒς–‘ΘΜ
ΒΡΒΞΒς–‘ΘΜ
Θ®2Θ©Β±![]() ±Θ§»τΚ· ΐ
±Θ§»τΚ· ΐ![]() ”κ
”κ![]() ΒΡΆΦœσ”–«“Ϋω”–“ΜΗωΫΜΒψ
ΒΡΆΦœσ”–«“Ϋω”–“ΜΗωΫΜΒψ![]() Θ§«σ
Θ§«σ![]() ΒΡ÷ΒΘ®Τδ÷–
ΒΡ÷ΒΘ®Τδ÷–![]() ±μ Ψ≤Μ≥§Ιΐ
±μ Ψ≤Μ≥§Ιΐ![]() ΒΡΉν¥σ’ϊ ΐΘ§»γ
ΒΡΉν¥σ’ϊ ΐΘ§»γ![]() Θ©.
Θ©.
≤ΈΩΦ ΐΨίΘΚ![]() .
.
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΙζΦ ―ß–Θ”≈―Γ - ΝΖœΑ≤αΝ–±μ - ‘ΧβΝ–±μ
Κΰ±± ΓΜΞΝΣΆχΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΤΫΧ® | Άχ…œ”–ΚΠ–≈œΔΨΌ±®Ή®«χ | Βγ–≈’©Τ≠ΨΌ±®Ή®«χ | …φάζ Ζ–ιΈό÷ς“ε”–ΚΠ–≈œΔΨΌ±®Ή®«χ | …φΤσ«÷»®ΨΌ±®Ή®«χ
ΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΒγΜΑΘΚ027-86699610 ΨΌ±®” œδΘΚ58377363@163.com