练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】通过随机询问100名性别不同的大学生是否爱好踢毽子，得到如下的列联表：

    随机变量经计算，统计量K2的观测值k0≈4.762，参照附表，得到的正确结论是(　　)

    A. 在犯错误的概率不超过5%的前提下，认为“爱好该项运动与性别有关”

    B. 在犯错误的概率不超过5%的前提下，认为“爱好该项运动与性别无关”

    C. 有97.5%以上的把握认为“爱好该项运动与性别有关”

    D. 有97.5%以上的把握认为“爱好该项运动与性别无关”

    【答案】A

    【解析】

    题目的条件中已经给出这组数据的观测值，只要把所给的观测值同节选的观测值表进行比较，发现它大于3.841，在犯错误的概率不超过5%的前提下，认为“爱好这项运动与性别有关”．

    解：由题意算得， 4.762＞3.841，参照附表，可得

    在犯错误的概率不超过5%的前提下，认为“爱好这项运动与性别有关”．

    故选：A．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】假设关于某种设备的使用年限(年)与所支出的维修费用 (万元)有如下统计：

    2

    3

    4

    5

    6

    2.2

    3.8

    5.5

    6.5

    7.0

    已知， . ，

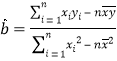    (1)求， ；

    (2)与具有线性相关关系，求出线性回归方程；

    (3)估计使用年限为10年时，维修费用约是多少？

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在直角坐标系中，曲线的参数方程为（为参数），其中.以原点为极点， 轴正半轴为极轴建立极坐标系，曲线的极坐标方程为.

    （1）求出曲线的普通方程和曲线的直角坐标方程；

    （2）已知曲线与交于， 两点，记点， 相应的参数分别为， ，当时，求的值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数f(x)的图像可以由y=cos2x的图像先纵坐标不变横坐标伸长到原来的2倍，再横坐标不变纵坐标伸长到原来的2倍，最后向右平移个单位而得到.

    ⑴求f(x)的解析式与最小正周期；

    ⑵求f(x)在x∈(0，π)上的值域与单调性.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】设椭圆 ()的一个焦点点为椭圆内一点,若椭圆上存在一点，使得，则椭圆的离心率的取值范围是（ ）

    A. B. C. D.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某公司生产一种产品，第一年投入资金1000万元，出售产品收入40万元，预计以后每年的投入资金是上一年的一半，出售产品所得收入比上一年多80万元，同时，当预计投入的资金低于20万元时，就按20万元投入，且当年出售产品收入与上一年相等.

    （1）求第年的预计投入资金与出售产品的收入；

    （2）预计从哪一年起该公司开始盈利？（注：盈利是指总收入大于总投入）

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数f(x)=2lnx-ax2,若α，β都属于区间[1,4]，且β-α=1，f(α)=f(β),则实数a的取值范围是________.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在平面直角坐标系中，曲线的参数方程为 (为参数），以为极点， 轴的非负半轴为极轴的极坐标系中，直线的极坐标方程为.

    （1）求曲线的极坐标方程；

    （2）设直线与曲线相交于两点，求的值.

    【答案】（1）曲线的极坐标方程为： ；（2）6.

    【解析】试题分析：（1）先根据三角函数平方关系消参数得曲线的普通方程，再根据化为极坐标方程；（2）将直线l的极坐标方程代入曲线的极坐标方程得，再根据求的值．

    试题解析：解:（1）将方程消去参数得，

    ∴曲线的普通方程为，

    将代入上式可得，

    ∴曲线的极坐标方程为： ． -

    （2）设两点的极坐标方程分别为,

    由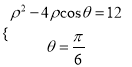消去得，

    根据题意可得是方程的两根，

    ∴，

    ∴．

    【题型】解答题
    【结束】
    23

    【题目】选修4—5：不等式选讲

    已知函数．

    (1)当时，求关于x的不等式的解集；

    (2)若关于x的不等式有解，求a的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知是公差不为零的等差数列，满足，且、、成等比数列.

    （1）求数列的通项公式；

    （2）设数列满足，求数列的前项和.

    【答案】（1）；（2）

    【解析】试题分析：（1）设等差数列 的公差为，由a3=7，且、、成等比数列．可得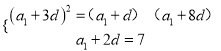，解之得即可得出数列的通项公式；

    2）由（1）得，则，由裂项相消法可求数列的前项和.

    试题解析：（1）设数列的公差为，且由题意得，

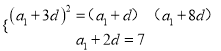    即 ，解得，

    所以数列的通项公式.

    （2）由（1）得

    ，

    .

    【题型】解答题
    【结束】
    18

    【题目】四棱锥的底面为直角梯形，，，，为正三角形.

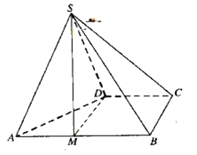
    （1）点为棱上一点，若平面，，求实数的值；

    （2）求点B到平面SAD的距离.

    查看答案和解析>>

    同步练习册答案